HULLÁMTERJEDÉSI ALAPOK
Abban, hogy rádióvevővel meteort tudunk észlelni, az ionoszférának van
jelentős szerepe. Ez a légkörnek kb. 50 km feletti tartománya. Itt a légkör
sűrűsége már rendkívül kicsi. Ez teszi lehetővé, hogy a kívülről jövő
kozmikus részecskék és sugárzások a levegő részecskéit ionizálják, s ezzel
elektromosan vezetővé tegyék. A néhány méternél rövidebb hullámhosszúságú
ultrarövid hullámok normális esetben áthaladnak az ionoszféra rétegein, és
csak különös esetben verődnek onnan vissza. Ezek a reflexiók többnyire az
ionoszféra 90-120 méter magasságban elhelyezkedő ún. E-rétegében történnek.
Okai a következők lehetnek:
- rendellenességek az ionoszférában (pl. napflerek hatására kialakuló
ionoszférikus viharok)
- sarki fény (ez is naptevékenység-függő)
- meteorbecsapódás (a meteorok 80-100 km magasan fékeződnek le ─ ez az E
rétegbe esik)
- az E-réteg sporadikus ionizációja (a sporadikus meteorok között a
nagyobb tömegűek aránya alacsonyabb, mint a rajmeteoroknál, ezért ezek
egy alacsony szintű állandó ionizációt hoznak létre)
Mivel az ultrarövid hullámok ─ szemben a hosszabbakkal ─ csak ilyenkor
verődnek vissza, alkalmasak a meteorok megfigyelésére.
Mint láttuk, a meteorok pályájuk mentén ioncsíkot húznak. Ezután a
részecskék hőmozgása, valamint a rekombináció miatt a nyom kiszélesedik,
töltéssűrűsége pedig csökken. Kétfajta meteornyomot különböztetünk meg
töltéssűrűségük szerint: A kis sűrűségű nyomok esetén a visszaverődést úgy
tekinthetjük, mintha különálló elektronokról történne. A vett jel hirtelen
éri el a maximumát, majd exponenciálisan csökken. Nagyobb elektronsűrűségű
nyomok esetén az elektronok egymás közötti hatását is figyelembe kell venni.
Úgy tekinthetjük, mint egy fémhengert. Ilyenkor a visszaverődő jel erőssége
nem kezd azonnal csökkenni, az adó másodpercekig is hallhatóvá válhat. A
nagyobb tömegű meteorok nagyobb töltéssűrűségű nyomot hoznak létre. Rajtagok
esetében a nagyobb tömegűek aránya magasabb, mint a sporadikusoknál, így
több nagy sűrűségű nyomot szolgáltatnak. A sporadikusok között rengeteg kis
meteor van. Ezek szinte állandó ionizációt hoznak létre, emiatt fontos
szerepet kapnak a nagy távolságú URH-átvitelben.
Érdemes kitérni arra, hogy a meteornyomok geometriai eloszlása hogyan
befolyásolja a megfigyelést. Az adó és vevő között becsapódó - mérete miatt
elvileg megfigyelhető - meteorok száma jóval nagyobb a valóban észlelteknél.
Egy érdekes geometriai következmény: azt gondolnánk, hogy a legtöbb
rádióvisszhang az adó és a vevő közötti főkörön levő meteorokról érkezik. Az
ilyen jel a valóságban nagyon ritka. Ehhez ugyanis annak kellene
teljesülnie, hogy a meteorpálya vízszintes legyen. Ez pedig ritkán fordul
elő. A legtöbb észlelt meteor a főkörtől oldalra eső térrészben van. A
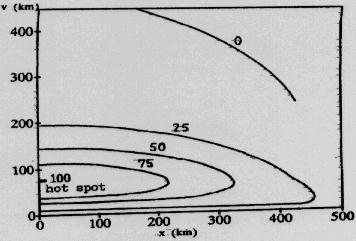
sporadikusok visszhanggyakorisági eloszlása a 4. ábrán látható. Mivel a
rajok pályairány szerinti eloszlása más és más a radiáns helyzetétől
függően, minden rajra meg lehetne szerkeszteni egy ilyen görbét. Ráadásul
általában nem egyetlen adó működik az észlelés sávjában. Azt a helyet,
ahonnan a legtöbb jel érkezik, a szaknyelv forró pontnak (hot spot) nevezi.
''4. ábra
A sporadikus meteorok visz-
szhang-eloszlása 1000 km-es
adó és vevőtávolság esetén.
(Az ábra a meteorészlelések
térbeli eloszlásának vízszin-
tes ─ a vevőn és az adón át-
fektetett gömbi főkörív cent-
rumára illeszkedő ─ síkra való
vetületének szintgörbéit mu-
tatja. A szintgörbéket az azo-
nos jelgyakoriságot szolgálta-
tó helyek e síkra való vetüle-
tei rajzolják ki. A vízszintes
tengelyen a gömbi főkör mentén
mért távolság, a függőleges
''tengelyen a főkör síkjától mért távolság van feltüntetve.)ď0
Az észlelhető meteornyomok magasságeloszlására is végeztek
megfigyeléseket az 50-es, 60-as években. Eszerint a megfigyelhető nyomok
magassága az észlelés frekvenciáját növelve csökken. Az amatőrök körében
használt 70-100 MHz-es tartományban az átlagos magasság 90 és 100 km között
van.
Miközben a meteorok végigsuhannak a légkörben, ioncsatornát hoznak létre.
A meteor fizikai tulajdonságai-
nak pontosabb megállapításához
a jel minél több jellemzőjére
''5. ábra
A visszhangot okozó meteorok
magasság szerinti eloszlása az
észlelési frekvencia függvényé-
ben 18, 36 és 70 MHz-en. A füg-
gőleges tengely az óránkénti
meteorszámot jelöli.
A talajszint feletti magasság
szükségünk van. Elsősorban a jel időtartamára, a jel amplitúdójára, de a jel
alakja is hasznos információt hordoz. Az alacsonysűrűségű meteorjel
(kevesebb mint 10^14 elektron méterenként) ugyanis az amplitúdójával
arányos, míg a nagysűrűségű a jel hosszával. Ez utóbbi nyom időtartama a
következőképpen alakul:
q *lambdaý
T = 7 * 10 ^-7 * -----------
D cos fi
ahol T = a jel időtartama,
q = az egy méterre eső elektronok száma,
lambda = a hullámhossz,
fi = a visszaverődés szöge,
D = a diffúziós állandó, ami függ a nyom magasságától.
Mint látjuk ez nagyon sok mindentől függ. A pontos töltéssűrűség
megállapítása a jelből alapos körültekintést és tapasztalatot igényel.
A megfigyelést 94,5 MHz-en végezzük (3,17 m hullámhosszon). Az
egyszerűség miatt feltételezzük, hogy a visszaverődés az adót a vevővel
összekötő gömbi főkör mentén történik 90 km magasságban, az egymástól 1000
km-re levő adó és a vevő felezőpontjában. A további egyszerűsítés végett
vízszintes meteorbeesést felétételezzünk. Ekkor a visszaverődési szög 79,8º;
ebben a magasságban a diffúziós állandó 3 mý/s.
A meteor töltéssűrűségéből lehet következtetni arra, hogy milyen fényes
meteortól származott. A meteor fényességét magnitúdóban mérjük. Hipparkhosz,
az ókori görög csillagász osztotta fel a csillagokat 6 nagyságrendre (a
magnitúdó görögül nagyságot jelent). A legfényesebb csillagokat sorolta az
egyes nagyságrendbe, a leghalványabbakat az hatosba. Ennél pontosabb
definícióra csak a változócsillagmegfigyelések kezdetekor volt szükség.
Ekkor definiálták pontosan a skálát. Eszerint két csillag
fényességkülönbsége magnitúdóban:
I1
m1 - m2 = -2,5log ----
I2
azaz 100-szoros intenzitás 5 magnitúdó különbségnek felel meg. Alapul a
sarkcsillag fényességét választották. Ennek 2,12 magnitúdós fényessége
definiálja a skálát. A meteor "rádiómagnitúdóját" az egyenletből kapjuk, ha
- 2 < MR < 5. Ez nagyjából megegyezik a vizuális fényességével. A fenti
feltételek mellett az egyenletekből a következő adatok adódnak:
┌──────────────┬──────┬───────┐
│MR (magnitúdó)│ q │ T(s) │
├──────────────┼──────┼───────┤
│ 5 │ 1,00│ 0,75 │
│ 4 │ 2,5 │ 1,87 │
│ 3 │ 6,3 │ 4,70 │
│ 2 │ 15,8 │ 11,82 │
│ 1 │ 39,8 │ 29,7 │
│ 0 │100 │ 74,60 │
│ -1 │250 │187,40 │
└──────────────┴──────┴───────┘ ''4. ábra
A sporadikus meteorok visz-
szhang-eloszlása 1000 km-es
adó és vevőtávolság esetén.
(Az ábra a meteorészlelések
térbeli eloszlásának vízszin-
tes ─ a vevőn és az adón át-
fektetett gömbi főkörív cent-
rumára illeszkedő ─ síkra való
vetületének szintgörbéit mu-
tatja. A szintgörbéket az azo-
nos jelgyakoriságot szolgálta-
tó helyek e síkra való vetüle-
tei rajzolják ki. A vízszintes
tengelyen a gömbi főkör mentén
mért távolság, a függőleges
''tengelyen a főkör síkjától mért távolság van feltüntetve.)ď0
Az észlelhető meteornyomok magasságeloszlására is végeztek
megfigyeléseket az 50-es, 60-as években. Eszerint a megfigyelhető nyomok
magassága az észlelés frekvenciáját növelve csökken. Az amatőrök körében
használt 70-100 MHz-es tartományban az átlagos magasság 90 és 100 km között
van.
Miközben a meteorok végigsuhannak a légkörben, ioncsatornát hoznak létre.
''4. ábra
A sporadikus meteorok visz-
szhang-eloszlása 1000 km-es
adó és vevőtávolság esetén.
(Az ábra a meteorészlelések
térbeli eloszlásának vízszin-
tes ─ a vevőn és az adón át-
fektetett gömbi főkörív cent-
rumára illeszkedő ─ síkra való
vetületének szintgörbéit mu-
tatja. A szintgörbéket az azo-
nos jelgyakoriságot szolgálta-
tó helyek e síkra való vetüle-
tei rajzolják ki. A vízszintes
tengelyen a gömbi főkör mentén
mért távolság, a függőleges
''tengelyen a főkör síkjától mért távolság van feltüntetve.)ď0
Az észlelhető meteornyomok magasságeloszlására is végeztek
megfigyeléseket az 50-es, 60-as években. Eszerint a megfigyelhető nyomok
magassága az észlelés frekvenciáját növelve csökken. Az amatőrök körében
használt 70-100 MHz-es tartományban az átlagos magasság 90 és 100 km között
van.
Miközben a meteorok végigsuhannak a légkörben, ioncsatornát hoznak létre.
 A meteor fizikai tulajdonságai-
nak pontosabb megállapításához
a jel minél több jellemzőjére
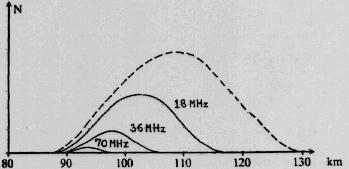
''5. ábra
A visszhangot okozó meteorok
magasság szerinti eloszlása az
észlelési frekvencia függvényé-
ben 18, 36 és 70 MHz-en. A füg-
gőleges tengely az óránkénti
meteorszámot jelöli.
A talajszint feletti magasság
szükségünk van. Elsősorban a jel időtartamára, a jel amplitúdójára, de a jel
alakja is hasznos információt hordoz. Az alacsonysűrűségű meteorjel
(kevesebb mint 10^14 elektron méterenként) ugyanis az amplitúdójával
arányos, míg a nagysűrűségű a jel hosszával. Ez utóbbi nyom időtartama a
következőképpen alakul:
q *lambdaý
T = 7 * 10 ^-7 * -----------
D cos fi
ahol T = a jel időtartama,
q = az egy méterre eső elektronok száma,
lambda = a hullámhossz,
fi = a visszaverődés szöge,
D = a diffúziós állandó, ami függ a nyom magasságától.
Mint látjuk ez nagyon sok mindentől függ. A pontos töltéssűrűség
megállapítása a jelből alapos körültekintést és tapasztalatot igényel.
A megfigyelést 94,5 MHz-en végezzük (3,17 m hullámhosszon). Az
egyszerűség miatt feltételezzük, hogy a visszaverődés az adót a vevővel
összekötő gömbi főkör mentén történik 90 km magasságban, az egymástól 1000
km-re levő adó és a vevő felezőpontjában. A további egyszerűsítés végett
vízszintes meteorbeesést felétételezzünk. Ekkor a visszaverődési szög 79,8º;
ebben a magasságban a diffúziós állandó 3 mý/s.
A meteor töltéssűrűségéből lehet következtetni arra, hogy milyen fényes
meteortól származott. A meteor fényességét magnitúdóban mérjük. Hipparkhosz,
az ókori görög csillagász osztotta fel a csillagokat 6 nagyságrendre (a
magnitúdó görögül nagyságot jelent). A legfényesebb csillagokat sorolta az
egyes nagyságrendbe, a leghalványabbakat az hatosba. Ennél pontosabb
definícióra csak a változócsillagmegfigyelések kezdetekor volt szükség.
Ekkor definiálták pontosan a skálát. Eszerint két csillag
fényességkülönbsége magnitúdóban:
I1
m1 - m2 = -2,5log ----
I2
azaz 100-szoros intenzitás 5 magnitúdó különbségnek felel meg. Alapul a
sarkcsillag fényességét választották. Ennek 2,12 magnitúdós fényessége
definiálja a skálát. A meteor "rádiómagnitúdóját" az egyenletből kapjuk, ha
- 2 < MR < 5. Ez nagyjából megegyezik a vizuális fényességével. A fenti
feltételek mellett az egyenletekből a következő adatok adódnak:
┌──────────────┬──────┬───────┐
│MR (magnitúdó)│ q │ T(s) │
├──────────────┼──────┼───────┤
│ 5 │ 1,00│ 0,75 │
│ 4 │ 2,5 │ 1,87 │
│ 3 │ 6,3 │ 4,70 │
│ 2 │ 15,8 │ 11,82 │
│ 1 │ 39,8 │ 29,7 │
│ 0 │100 │ 74,60 │
│ -1 │250 │187,40 │
└──────────────┴──────┴───────┘
A meteor fizikai tulajdonságai-
nak pontosabb megállapításához
a jel minél több jellemzőjére
''5. ábra
A visszhangot okozó meteorok
magasság szerinti eloszlása az
észlelési frekvencia függvényé-
ben 18, 36 és 70 MHz-en. A füg-
gőleges tengely az óránkénti
meteorszámot jelöli.
A talajszint feletti magasság
szükségünk van. Elsősorban a jel időtartamára, a jel amplitúdójára, de a jel
alakja is hasznos információt hordoz. Az alacsonysűrűségű meteorjel
(kevesebb mint 10^14 elektron méterenként) ugyanis az amplitúdójával
arányos, míg a nagysűrűségű a jel hosszával. Ez utóbbi nyom időtartama a
következőképpen alakul:
q *lambdaý
T = 7 * 10 ^-7 * -----------
D cos fi
ahol T = a jel időtartama,
q = az egy méterre eső elektronok száma,
lambda = a hullámhossz,
fi = a visszaverődés szöge,
D = a diffúziós állandó, ami függ a nyom magasságától.
Mint látjuk ez nagyon sok mindentől függ. A pontos töltéssűrűség
megállapítása a jelből alapos körültekintést és tapasztalatot igényel.
A megfigyelést 94,5 MHz-en végezzük (3,17 m hullámhosszon). Az
egyszerűség miatt feltételezzük, hogy a visszaverődés az adót a vevővel
összekötő gömbi főkör mentén történik 90 km magasságban, az egymástól 1000
km-re levő adó és a vevő felezőpontjában. A további egyszerűsítés végett
vízszintes meteorbeesést felétételezzünk. Ekkor a visszaverődési szög 79,8º;
ebben a magasságban a diffúziós állandó 3 mý/s.
A meteor töltéssűrűségéből lehet következtetni arra, hogy milyen fényes
meteortól származott. A meteor fényességét magnitúdóban mérjük. Hipparkhosz,
az ókori görög csillagász osztotta fel a csillagokat 6 nagyságrendre (a
magnitúdó görögül nagyságot jelent). A legfényesebb csillagokat sorolta az
egyes nagyságrendbe, a leghalványabbakat az hatosba. Ennél pontosabb
definícióra csak a változócsillagmegfigyelések kezdetekor volt szükség.
Ekkor definiálták pontosan a skálát. Eszerint két csillag
fényességkülönbsége magnitúdóban:
I1
m1 - m2 = -2,5log ----
I2
azaz 100-szoros intenzitás 5 magnitúdó különbségnek felel meg. Alapul a
sarkcsillag fényességét választották. Ennek 2,12 magnitúdós fényessége
definiálja a skálát. A meteor "rádiómagnitúdóját" az egyenletből kapjuk, ha
- 2 < MR < 5. Ez nagyjából megegyezik a vizuális fényességével. A fenti
feltételek mellett az egyenletekből a következő adatok adódnak:
┌──────────────┬──────┬───────┐
│MR (magnitúdó)│ q │ T(s) │
├──────────────┼──────┼───────┤
│ 5 │ 1,00│ 0,75 │
│ 4 │ 2,5 │ 1,87 │
│ 3 │ 6,3 │ 4,70 │
│ 2 │ 15,8 │ 11,82 │
│ 1 │ 39,8 │ 29,7 │
│ 0 │100 │ 74,60 │
│ -1 │250 │187,40 │
└──────────────┴──────┴───────┘