FORGÓ LYUKAKON ÁT ... HOVÁ?
Így nem sikerült alagutat csinálni. De ne csüggedjünk. Van a
relativitáselméletben jobb lyuk is, de annak már fel sem írom a geometriai
képletét. Ez az ún. Kerr-megoldás. Időben nem változó, forgásszimmetrikus
geometria. Van neki M tömege, amiből megint megcsinálhatjuk m-et, és van J
perdülete, amiből csinálhatunk egy másik hosszat: a = J/Mc. Két eset van,
vagy a a nagyobb, vagy m. A második esetben a geometria fekete lyuk, de az
elsőben nem.
Ez nem meglepő. Ha m a nagyobb, a tömeg dominál a forgás felett, ha a
nagyobb, a forgás a tömeg felett. Ha most azt keressük, hol a tömeg, azt
kell mondanunk, hogy ott, ahol a téridő a leggörbültebb. Nos, most a
görbület végtelen nagy egy a sugarú karikán. Remek: egy forgó csillag omlott
össze, és a "röpítőerő" (ami megint csak nem erő) ide kente az összehúzódó
anyagot. Ha pontosan megcélozzuk a karika közepét, nem ütközünk a karikába,
nem lép fel végtelen nagy árapályhatás, és átjuthatunk. Jó ez nekünk
valamire?
Először intézzük el az a > m esetet, amikor a geometria nem fekete lyuk.
Van valahol egy forgó karika: ha a karikához nagyon közel megyünk, széttép,
ha nem, nem. Van itt valami izgalmas? Van bizony, habár ezt az olvasó most
egyszerűen el kell higyje, mert képletet nem adtam. Kevéssel a gyűrű síkján
belül (hogy a "belül" itt mit jelent, arra mindjárt kitérünk) a geometria
olyanná válik, hogy a test mozgása közben dsý még úgy is tud negatív lenni,
hogy sem r, sem ę, sem t (!) nem változik, csak ě. De ě-ben 360º-ot
körbejárva ugyanoda jutunk, tehát az űrhajós egyszerre jelen lehet egy egész
kör minden pontjában, és önmagával találkozhat! Ez ocsmányságnak tűnik.
Kicsit még beljebb már visszafelé is lehet menni időben: itt az időutazás.
Nos, ez sokaknak nem tetszik. (Nekem sem.) Ráadásul senki sem
bizonyította, hogy ez lenne az egyetlen lehetséges geometria, amelyet M
tömegű és J perdületű forrás hoz létre. Hátha ez a gravitációs egyenletek
egy "hamis" megoldása: olyan geometria, amely a tényleges összeomlási
folyamatban soha sem alakul ki (habár hogy miért nem, azt csak akkor tudjuk
meg, ha számítással az egész folyamatot végig tudjuk követni). Minden
további nélkül meglehet. És akik ezt hiszik, azok egy elvet próbáltak
megfogalmazni. Ez a Kozmikus Cenzúra elve: "A természetben nincsenek
meztelen szingularitások." (A szingularitás a végtelen görbület, ami itt a
karikán van, és akkor meztelen, ha nem fedi el az illedelmesen a külvilág
elől egy fény által át nem járható horizont.) Ha a Kozmikus Cenzor működik a
természetben, akkor e zavaró forgó karika nem fejlődik ki, az űrhajós nem
találkozik magával, és nem utazik a múltba. (A Kozmikus Cenzor nevet
angolszász fizikusok találták ki, és a brit királyi cenzor a filmeket és
színdarabokat cenzúrázza oly módon, hogy a nyíltszíni meztelenkedést gátolja
meg.)
Remek, rend és tisztesség van. Namost nézzük meg a kis perdületű Kerr-
megoldást (az a < m esetet). Azt horizont veszi körül (két rétegben), a
Kozmikus Cenzornak nincs dolga vele. Azért nézzük meg, milyen fekete lyuk.
Aki nem akarja elhinni, ami most jön, annak adhatok eredeti forrást, [30] de
ha nem fizikus, sok haszna nem lesz belőle. Néhány dolgot megpróbálok
rajzzal illusztrálni, de euklideszi síkon szinte lehetetlen hűen ábrázolni
egy ilyen görbült geometriát.
A gömb alakú (Schwarzschild) fekete lyuknál megtanultuk, hogy a
horizonton befelé át lehet esni (csak a kívül maradók ezt nem látják). Ott
ez öngyilkosság volt, de most ha pontosan középre célzunk, nem jutunk nagyon
közel a végtelen görbülethez, tehát az árapályhatás véges marad. Üljünk
űrhajóba, célozzuk meg a (nem látszó) gyűrű közepét, és induljunk meg.
Először elég nagy kezdősebességgel. Amit várunk, az az, hogy átjutunk a
horizontokon, r egyre csökken, azután elérjük a középpontot. Addig r csökken
és a ę pólustávolság 0º, utána kibukkanunk a gyűrű túloldalán, mivel a túlsó
póluson emelkedünk, tehát r nő és ę = 180º. Ez történik minden szokásos
gyűrűn való áthaladáskor, lásd a 10. ábra a) részét. Hogy azután mi lesz az
emelkedés vége, azt ki kell számítani.
Ezzel szemben az történik, hogy - mivel r = 0-nál, a középpontban semmi
sem történik - r tovább csökken, miközben ę 0º marad. Nem a gyűrű túlfelére
jutottunk, a "déli" pólushoz, hanem megyünk a gyűrű belsejébe. E szót
használtuk az előbb. Hogy ezt hogyan rajzoljam le, azt még egy
grafikusművésztől sem kérdezhetem meg; erőfeszítésem eredménye a 10. ábra b)
része. Megyünk tovább; r már negatív, és csökken tovább, ahogyan szállunk
tovább befelé, még mindig az északi pólus alatt. Mi lesz ebből, és hová
jutottunk?
Alighanem a Másvilágba. Ugyanis a horizontok ugyan körülveszik a gyűrűt,
de persze a külsején, nem a belsején. Ezért r negatív értékeinél bármilyen
messze eljuthatunk akadály nélkül. És amikor r már nagyon nagy negatív
érték, a geometria megint hasonlóvá kezd válni (14)-hez.
De m/r negatív: ez épp olyan, mint mikor r pozitív, de m negatív.
Visszanézünk, és egy taszító tömeget látunk! Ez egy fehér lyuk: nem nyel,
hanem taszít. Ilyent mi, itt ahol vagyunk, nem látunk.
Hacsak a fénylő kvazárok nem fehér lyukak; de valószínűleg nem, [12] és
még a legközelebbi is 2 milliárd évre van. Amit szerencsés utazásunk végén
látunk, az egészen más, mint ahonnan elindultunk. Itt az első olyan lyuk,
mely tulajdonképpen alagút. Hogy hová vezet, azt még vizsgálni kell.
10. ábra
Mozgás közönséges karika (a)
és Kerr-karika (b) táján
Közönséges karikán átmehetünk és meg is
kerülhetjük, mégis ugyanoda jutunk. Kerr-
karika esetén, melyet a karikára összeom-
lott forgó anyag görbít ki a téridőben
(?), az északi pólusból csak a karikát
megkerülve jutunk a délibe (2. útvonal);
a gyűrűn át (1. útvonal) tovább szállunk
lefelé, és egy "más világba" jutunk bel-
ül. A számítások szerint ott is végtele-
nig utazhatunk, de onnan nézve a lyuk
fehér (taszít). Nem tudjuk. hogy ilyen
geometriát tényleg létre tud-e hozni az
összeomló anyag, de a geometria a gravi-
tációs törvénynek megfelel.
A Kerr-lyuk talán mindenhová vezet. Bizonyos kezdősebességű mozgásnál a
forgás (már a gyűrűn belülről) visszadobja az űrhajót, és az belülről átjut
a horizonton. (Hogy ilyen hogyan történhet meg, ahhoz most néhány új fejezet
kellene, aminek nem lenne hosszadalmasságával összemérhető haszna. A
tisztelt olvasónak azt mondhatom, amit egy hitvita egyik résztvevője mondott
a másiknak a vitatott teológiai pontról: ha már az eddigieket elfogadta, azt
is elfogadhatta volna éppúgy. Egyébként Kaufmann műve [31] e furcsaságot
ábrákon mutatja be.) Szóval az űrhajó kijut az északi pólusnál a horizonton,
és pozitív r-eknél emelkedik. Csakhogy hamarabb jut ki, mint ahogyan bement.
Ez megint időutazás. Vagy elhisszük, és bízunk abban, hogy a
paradoxonokat később a tudomány majd megoldja, vagy azt kell mondanunk, hogy
nem odajutott ki, ahonnan bement. De ugyanolyan magasan van. Nos, tegyük fel
(tegyük?), hogy a Világ több példányban létezik, az egyikből ment be, és a
másikba jött ki. Node akkor végtelen sok világ kell, mert ha csak kettő
volna, megismételhetnők az utazást: be a másodikból, aki az elsőbe,
hamarább, mint az első bemenetkor.
Nos, mit higgyünk? Esetleg a Kerr-lyuk az, amely a magasabb dimenziós tér
végtelen sok hiperfelületét összeköti? Vagy, ha ez túlzásnak tűnik, higgyük
inkább el az időutazást? Vagy egyiket sem, és eresszük rá a Kozmikus
Cenzort? Ez volna a legóvatosabb eljárás. Csakhogy a cenzor nem illetékes,
ha a meztelenkedés zártkörű, és itt van horizont. Más szóval, az elvet ki
kellene terjeszteni. Nosza. De akkor baj lesz. Ugyanis bizonyították, hogy a
kis perdületű Kerr-megoldás az egyetlen (töltetlen stb.) reguláris horizontú
fekete lyuk megoldás. (A "reguláris" szó itt azt jelenti, hogy a többi még
rosszabb.) Ha ezt kizárjuk, akkor félő, hogy a forgó csillag összeomlásához
nem marad végállapot, ami viszont nem lehet. Ez egy máig élő dilemma. Én nem
tudom a megoldást (pedig magam is dolgozom ilyen területen). Nem azért
mondtam el, hogy az olvasó találja ki a választ. Előbb-utóbb a specialisták
valahogyan megválaszolják a kérdést. Lehet pl. hogy a rendkívül sűrű forgó
anyag gravitációs hatása addig fúrja a téridő-kontinuumot, amíg valahol
messzebb is kilyukasztja, és így többszörözi meg a kijáratot. (Ez legalább
méltóságteljesen hangzik.) Csak azt mondom: íme, a gyorsan mozgó sűrű anyag
elő tudhat állítani ahhoz hasonló hátsólépcsőket, mint amelyekről
fantáziáltunk.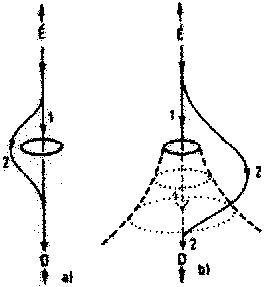 10. ábra
Mozgás közönséges karika (a)
és Kerr-karika (b) táján
Közönséges karikán átmehetünk és meg is
kerülhetjük, mégis ugyanoda jutunk. Kerr-
karika esetén, melyet a karikára összeom-
lott forgó anyag görbít ki a téridőben
(?), az északi pólusból csak a karikát
megkerülve jutunk a délibe (2. útvonal);
a gyűrűn át (1. útvonal) tovább szállunk
lefelé, és egy "más világba" jutunk bel-
ül. A számítások szerint ott is végtele-
nig utazhatunk, de onnan nézve a lyuk
fehér (taszít). Nem tudjuk. hogy ilyen
geometriát tényleg létre tud-e hozni az
összeomló anyag, de a geometria a gravi-
tációs törvénynek megfelel.
A Kerr-lyuk talán mindenhová vezet. Bizonyos kezdősebességű mozgásnál a
forgás (már a gyűrűn belülről) visszadobja az űrhajót, és az belülről átjut
a horizonton. (Hogy ilyen hogyan történhet meg, ahhoz most néhány új fejezet
kellene, aminek nem lenne hosszadalmasságával összemérhető haszna. A
tisztelt olvasónak azt mondhatom, amit egy hitvita egyik résztvevője mondott
a másiknak a vitatott teológiai pontról: ha már az eddigieket elfogadta, azt
is elfogadhatta volna éppúgy. Egyébként Kaufmann műve [31] e furcsaságot
ábrákon mutatja be.) Szóval az űrhajó kijut az északi pólusnál a horizonton,
és pozitív r-eknél emelkedik. Csakhogy hamarabb jut ki, mint ahogyan bement.
Ez megint időutazás. Vagy elhisszük, és bízunk abban, hogy a
paradoxonokat később a tudomány majd megoldja, vagy azt kell mondanunk, hogy
nem odajutott ki, ahonnan bement. De ugyanolyan magasan van. Nos, tegyük fel
(tegyük?), hogy a Világ több példányban létezik, az egyikből ment be, és a
másikba jött ki. Node akkor végtelen sok világ kell, mert ha csak kettő
volna, megismételhetnők az utazást: be a másodikból, aki az elsőbe,
hamarább, mint az első bemenetkor.
Nos, mit higgyünk? Esetleg a Kerr-lyuk az, amely a magasabb dimenziós tér
végtelen sok hiperfelületét összeköti? Vagy, ha ez túlzásnak tűnik, higgyük
inkább el az időutazást? Vagy egyiket sem, és eresszük rá a Kozmikus
Cenzort? Ez volna a legóvatosabb eljárás. Csakhogy a cenzor nem illetékes,
ha a meztelenkedés zártkörű, és itt van horizont. Más szóval, az elvet ki
kellene terjeszteni. Nosza. De akkor baj lesz. Ugyanis bizonyították, hogy a
kis perdületű Kerr-megoldás az egyetlen (töltetlen stb.) reguláris horizontú
fekete lyuk megoldás. (A "reguláris" szó itt azt jelenti, hogy a többi még
rosszabb.) Ha ezt kizárjuk, akkor félő, hogy a forgó csillag összeomlásához
nem marad végállapot, ami viszont nem lehet. Ez egy máig élő dilemma. Én nem
tudom a megoldást (pedig magam is dolgozom ilyen területen). Nem azért
mondtam el, hogy az olvasó találja ki a választ. Előbb-utóbb a specialisták
valahogyan megválaszolják a kérdést. Lehet pl. hogy a rendkívül sűrű forgó
anyag gravitációs hatása addig fúrja a téridő-kontinuumot, amíg valahol
messzebb is kilyukasztja, és így többszörözi meg a kijáratot. (Ez legalább
méltóságteljesen hangzik.) Csak azt mondom: íme, a gyorsan mozgó sűrű anyag
elő tudhat állítani ahhoz hasonló hátsólépcsőket, mint amelyekről
fantáziáltunk.
10. ábra
Mozgás közönséges karika (a)
és Kerr-karika (b) táján
Közönséges karikán átmehetünk és meg is
kerülhetjük, mégis ugyanoda jutunk. Kerr-
karika esetén, melyet a karikára összeom-
lott forgó anyag görbít ki a téridőben
(?), az északi pólusból csak a karikát
megkerülve jutunk a délibe (2. útvonal);
a gyűrűn át (1. útvonal) tovább szállunk
lefelé, és egy "más világba" jutunk bel-
ül. A számítások szerint ott is végtele-
nig utazhatunk, de onnan nézve a lyuk
fehér (taszít). Nem tudjuk. hogy ilyen
geometriát tényleg létre tud-e hozni az
összeomló anyag, de a geometria a gravi-
tációs törvénynek megfelel.
A Kerr-lyuk talán mindenhová vezet. Bizonyos kezdősebességű mozgásnál a
forgás (már a gyűrűn belülről) visszadobja az űrhajót, és az belülről átjut
a horizonton. (Hogy ilyen hogyan történhet meg, ahhoz most néhány új fejezet
kellene, aminek nem lenne hosszadalmasságával összemérhető haszna. A
tisztelt olvasónak azt mondhatom, amit egy hitvita egyik résztvevője mondott
a másiknak a vitatott teológiai pontról: ha már az eddigieket elfogadta, azt
is elfogadhatta volna éppúgy. Egyébként Kaufmann műve [31] e furcsaságot
ábrákon mutatja be.) Szóval az űrhajó kijut az északi pólusnál a horizonton,
és pozitív r-eknél emelkedik. Csakhogy hamarabb jut ki, mint ahogyan bement.
Ez megint időutazás. Vagy elhisszük, és bízunk abban, hogy a
paradoxonokat később a tudomány majd megoldja, vagy azt kell mondanunk, hogy
nem odajutott ki, ahonnan bement. De ugyanolyan magasan van. Nos, tegyük fel
(tegyük?), hogy a Világ több példányban létezik, az egyikből ment be, és a
másikba jött ki. Node akkor végtelen sok világ kell, mert ha csak kettő
volna, megismételhetnők az utazást: be a másodikból, aki az elsőbe,
hamarább, mint az első bemenetkor.
Nos, mit higgyünk? Esetleg a Kerr-lyuk az, amely a magasabb dimenziós tér
végtelen sok hiperfelületét összeköti? Vagy, ha ez túlzásnak tűnik, higgyük
inkább el az időutazást? Vagy egyiket sem, és eresszük rá a Kozmikus
Cenzort? Ez volna a legóvatosabb eljárás. Csakhogy a cenzor nem illetékes,
ha a meztelenkedés zártkörű, és itt van horizont. Más szóval, az elvet ki
kellene terjeszteni. Nosza. De akkor baj lesz. Ugyanis bizonyították, hogy a
kis perdületű Kerr-megoldás az egyetlen (töltetlen stb.) reguláris horizontú
fekete lyuk megoldás. (A "reguláris" szó itt azt jelenti, hogy a többi még
rosszabb.) Ha ezt kizárjuk, akkor félő, hogy a forgó csillag összeomlásához
nem marad végállapot, ami viszont nem lehet. Ez egy máig élő dilemma. Én nem
tudom a megoldást (pedig magam is dolgozom ilyen területen). Nem azért
mondtam el, hogy az olvasó találja ki a választ. Előbb-utóbb a specialisták
valahogyan megválaszolják a kérdést. Lehet pl. hogy a rendkívül sűrű forgó
anyag gravitációs hatása addig fúrja a téridő-kontinuumot, amíg valahol
messzebb is kilyukasztja, és így többszörözi meg a kijáratot. (Ez legalább
méltóságteljesen hangzik.) Csak azt mondom: íme, a gyorsan mozgó sűrű anyag
elő tudhat állítani ahhoz hasonló hátsólépcsőket, mint amelyekről
fantáziáltunk.