GÖDÖR ÉS LYUK
Hogy ezt ki-ki elhiszi-e, az az ő dolga. Azt, hogy ilyen helyekről a fény
sem tud kijönni, már Laplace megmondta a XVIII. sz. legvégén (és képlete
pontosan r = 2m volt), de most a kijelentés súlyosabb, mert a fény a
leggyorsabb hatás, tehát 2m alól semmi sem jön ki. Az eredményt a
rendelkezésünkre álló legmegbízhatóbb gravitációs törvényből kaptuk, és
ennél jobbat nem tudunk. Fizikusok közt kevés a kétely, hogy ha égitestek
anyagát sikerülne ilyen kicsire összepréselni, akkor tényleg kialakul e
nagyon furcsa térrész. Előfordult ugyan, hogy filozófus megpróbálta ezt
filozófiai alapon kétségbe vonni, [29] de hát ez már megint az I. részben
említett probléma. A természet törvényeit csak a természet vizsgálatából
lehet kitalálni. Persze, ha egy törvény nagyon furcsa (vagy pláne paradox)
eredményeket ad, akkor nem árt a törvényt még egyszer ellenőrizni. De a
törvény van (vagy nincs); nem alku tárgya.
A filozófust azért zavarta a "bezárulás", mert úgy érezte, hogy sérti az
elvet, amely szerint a mozgás az anyag elválaszthatatlan sajátsága. De -
látszólag - van még nagyobb baj is. Képzeljük el, hogy ennyire összeomlott
egy csillag (ténylegesen ponttá, mert láttuk, hogy anyaga 2m alatt sehol sem
állhat meg); ott van egy "nyelő". Beejtünk egy követ (vagy egy zseblámpát),
és figyeljük. Mit várunk?
Azt, hogy gyorsulva esik. Meghatározva a legegyenesebb vonalakat a (14)
geometriában, sajátidőben szépen ki is adódik pont ugyanazon esési törvény,
mint Newtonnál. De mikor 2m alá kerül, végleg eltűnik! (Mivelhogy onnan már
semmi ki nem jön.) Mi van az anyag megmaradásának törvényével? Azt ugyan
bárki állíthatja, hogy még ott van, de mit jelent valami olyannak a
létezése, amit soha semmilyen módon sem észlelhetünk?
Nos, a modern fizikában nem árt kissé óvatosnak lenni: mit jelent az
anyag megmaradása? Az anyagnak vannak megmaradó és változó adatai. De
legjobb tudomásunk szerint az elektromos töltés megmarad; tegyünk töltést
zseblámpákra, és akkor az nem illene, hogy eltűnjön.
Nem is teszi. És ha ez meglepő a fentebb mondottak után, a 9. ábra
szemlélteti. A valóság még meglepőbb. Az a) ábra mutatja, hogyan változik az
eső test r távolsága a sajátidőben (amit a rátett óra mér). Semmi furcsa. De
leirhatjuk az esést a t időben is (amit a kint álló, épp elmellőzött óra
mutat). Ez a b) ábra. A test az r = 2m horizonthoz (látóhatárhoz) közeledve
fokozatosan megáll, és soha nem jut be.
Bejut vagy nem? Melyik állítás az igaz? Mindkettő! A beeső test a
horizontot t = végtelenben éri el, tehát egyetlen kívül maradó megfigyelő
sem láthatja soha bejutni. A vele esők viszont igen. Az, hogy bejut-e majd,
attól függ, mit jelent a "majd", vagy a jövő idő.
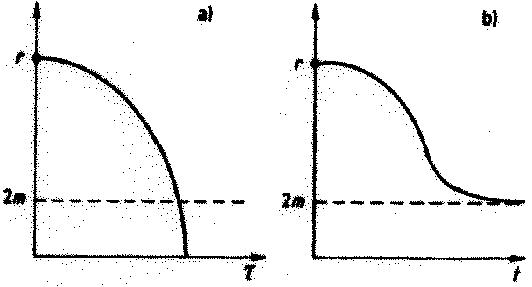9. ábra
Fekete lyukba eső űrhajó pályája:
a) saját órája, b) a külső megfigyelő órája szerint
A szaggatott vonal a horizont. Az űrhajós tapasztalata szerint
véges idő alatt eléri a középpontot (ahol gömbszimmetrikus
lyukban az árapály széttépi). Viszont a kívül álló megfigyelő
órája végtelen időt mutatna a horizont elérésekor. A jelenség
oka az időmérés függése a helyi geometriától és a sebességtől.
A furcsaság oka a relativisztikus időlassulás, mely r = 2m-nél végtelen
nagy. A paradoxon elmúlt: a kívül maradók számára a töltött zseblámpa soha
sem tűnik el (habár egyre infravörösebb); a befelé esők számára szintén nem.
Ha a kívül maradó időnként azt hiszi, hogy befelé esik, akkor lehetetlen
eredményekre jut, de annak, hogy milyen módokon lehet tévhitekbe esni, nem
sok köze van a fizikához. Vegyük észre, hogy e paradoxon a Zénóéhoz
hasonlóan oldódott fel: egyszerűen még végtelen sok t sem fedi le az eső
test teljes történetét. Hogy bonyolítsuk az ügyet, ha a külső megfigyelő nem
nézi a beeső töltött zseblámpát, hanem radarral figyeli, egy idő múlva
teljesen eltűnik az a radarernyőről. (A beeső lámpát a beeső fény a
horizonton belül éri utól, és onnan már hiába verődik vissza.) De ez már nem
elvi kérdés: nem ismerek olyan általános elvet, amely szerint anyag nem
tűnhet el radarernyőkről.
Fentiek szerint a ponttömeg minden ráesőt elnyel (sajátidőben), és onnan
semmi sem jön ki. Tehát lyuk és fekete. Egyéb görbületek csak gödrök: az
anyagot vonzzák, de azt azért onnan ki lehet szedni.
Nos: az anyag létrehozott egy lyukat a téridőn. Erre vártunk.
Megtörténik-e ez, és átvezet-e egy alagúton valahová máshová? Igen és nem. A
lyuk kialakul. Ehhez a Nap tömege ugyan nem elég, ha majd a Nap, 5,5
milliárd év múlva, kihűl, összehúzódása fehér törpeként megáll. De
néhányszor nagyobb tömeg már elég. [25] (Hogy pontosan mekkora, az nagyon
sok mindentől függ, pl. a magerők még ismeretlen részleteitől is.) Ekkora
csillagok ritkák, de vannak; általános vélemény szerint a kiégő csillag
tömegétől függ, hogy a szupernóva-kitörés végén neutroncsillag vagy fekete
lyuk marad-e vissza.
De, sajnos, a lyuk a teljes pusztulásba vezet. Közepén ott a pontszerű
tömeg, és minden egyre közelebb jut hozzá. Ennek során pedig egyre erősebb
árapályjelenség lép fel: a test különböző részei, különböző távolságra lévén
más-más pályán akarnának mozogni, és ez széttépi a testet. Bármilyen szilárd
is, a középpontot egyre jobban megközelítve valahol minden szétszakad és
elpusztul. A lyukaknak nincs kijárata. (A mindennapi életben a kijárat
nélküli lyuk mindig gödör. Most láttunk ellenpéldát. Íme, egy lejárat az
Alvilágba.)
Bizonyos kvantumelméleti számítások szerint az ilyen lyuk is sugárzással
eltűnik, csillagnyi tömeg esetén 10^63 év(!) alatt. Akkor szigorúan véve ez
is csak gödör lenne. De ez egyrészt finomkodás, másrészt még bizonytalanság
van abban, hogyan kell használni a kvantumelméletet görbült téridőben.
Egyébként nem gazdaságos most alakzatokat aszerint megkülönböztetni, mi lesz
velük 10^63 év után.
9. ábra
Fekete lyukba eső űrhajó pályája:
a) saját órája, b) a külső megfigyelő órája szerint
A szaggatott vonal a horizont. Az űrhajós tapasztalata szerint
véges idő alatt eléri a középpontot (ahol gömbszimmetrikus
lyukban az árapály széttépi). Viszont a kívül álló megfigyelő
órája végtelen időt mutatna a horizont elérésekor. A jelenség
oka az időmérés függése a helyi geometriától és a sebességtől.
A furcsaság oka a relativisztikus időlassulás, mely r = 2m-nél végtelen
nagy. A paradoxon elmúlt: a kívül maradók számára a töltött zseblámpa soha
sem tűnik el (habár egyre infravörösebb); a befelé esők számára szintén nem.
Ha a kívül maradó időnként azt hiszi, hogy befelé esik, akkor lehetetlen
eredményekre jut, de annak, hogy milyen módokon lehet tévhitekbe esni, nem
sok köze van a fizikához. Vegyük észre, hogy e paradoxon a Zénóéhoz
hasonlóan oldódott fel: egyszerűen még végtelen sok t sem fedi le az eső
test teljes történetét. Hogy bonyolítsuk az ügyet, ha a külső megfigyelő nem
nézi a beeső töltött zseblámpát, hanem radarral figyeli, egy idő múlva
teljesen eltűnik az a radarernyőről. (A beeső lámpát a beeső fény a
horizonton belül éri utól, és onnan már hiába verődik vissza.) De ez már nem
elvi kérdés: nem ismerek olyan általános elvet, amely szerint anyag nem
tűnhet el radarernyőkről.
Fentiek szerint a ponttömeg minden ráesőt elnyel (sajátidőben), és onnan
semmi sem jön ki. Tehát lyuk és fekete. Egyéb görbületek csak gödrök: az
anyagot vonzzák, de azt azért onnan ki lehet szedni.
Nos: az anyag létrehozott egy lyukat a téridőn. Erre vártunk.
Megtörténik-e ez, és átvezet-e egy alagúton valahová máshová? Igen és nem. A
lyuk kialakul. Ehhez a Nap tömege ugyan nem elég, ha majd a Nap, 5,5
milliárd év múlva, kihűl, összehúzódása fehér törpeként megáll. De
néhányszor nagyobb tömeg már elég. [25] (Hogy pontosan mekkora, az nagyon
sok mindentől függ, pl. a magerők még ismeretlen részleteitől is.) Ekkora
csillagok ritkák, de vannak; általános vélemény szerint a kiégő csillag
tömegétől függ, hogy a szupernóva-kitörés végén neutroncsillag vagy fekete
lyuk marad-e vissza.
De, sajnos, a lyuk a teljes pusztulásba vezet. Közepén ott a pontszerű
tömeg, és minden egyre közelebb jut hozzá. Ennek során pedig egyre erősebb
árapályjelenség lép fel: a test különböző részei, különböző távolságra lévén
más-más pályán akarnának mozogni, és ez széttépi a testet. Bármilyen szilárd
is, a középpontot egyre jobban megközelítve valahol minden szétszakad és
elpusztul. A lyukaknak nincs kijárata. (A mindennapi életben a kijárat
nélküli lyuk mindig gödör. Most láttunk ellenpéldát. Íme, egy lejárat az
Alvilágba.)
Bizonyos kvantumelméleti számítások szerint az ilyen lyuk is sugárzással
eltűnik, csillagnyi tömeg esetén 10^63 év(!) alatt. Akkor szigorúan véve ez
is csak gödör lenne. De ez egyrészt finomkodás, másrészt még bizonytalanság
van abban, hogyan kell használni a kvantumelméletet görbült téridőben.
Egyébként nem gazdaságos most alakzatokat aszerint megkülönböztetni, mi lesz
velük 10^63 év után.