A SÍK TÉRIDŐ
1908 óta tudjuk, hogy nincs abszolút tér. Mindenkinek van saját
3-dimenziós tere és 1-dimenziós ideje, de az csak reá tartozik. 1881-ben
Michelson megpróbálta megmérni a Föld sebességét az abszolút térben,
sikertelenül. Az ötlet lényege az volt, hogy a fény valamihez képest terjed
c sebességgel; nyilván az abszolút térben. Egy ún. interferométer karjain
futtatta végig a fényt két irányba, azután elfordította a karokat, s megint.
Ha az interferométer nem áll, akkor - gondolta - a két kar mentén nem azonos
idő alatt fut végig a fény, és a futási idő a karok irányától függ.
Elfordítás után tehát az interferenciamintázat megváltozik. Műszere 3 km/s
sebességet már kimutatott volna, de semmit sem talált. Ez nagy meglepetés
volt; 3 magyarázattal lehetett próbálkozni.
1. A Föld nem mozog a térben. Ez teljesen hihetetlen, hiszen kering a Nap
körül (30 km/s), az a Tejút középpontja körül és így tovább.
2. A Föld magával viszi az "étert ", amelyben a fény rezgésként terjed.
Ez lehetetlen, mert akkor a keringő bolygók súrlódnának az éterben,
és azt látni lehetne a bolygók mozgásán, aminek nyoma sincs.
3. A testek mozgásuk irányában megrövidülnek. Ez volt Lorentz ötlete: egy
sqrt (1-vý/cý) arányú rövidülés épp kiegyenlítette volna a mozgás
hatását, és minden további nélkül lehetséges, mert a részecskék közti
erő terjedését befolyásolja a mozgás. (A részleteket az olvasó
megtalálja máshol; itt most nem ez a fő kérdés.)
Jó ötlet volt, csakhogy ha ez minden testre egyetemes összehúzódás, akkor
sehogyan sem lehet megmérni a testek igazi hosszát, mert a mérőrudak is
összehúzódnak. 1905-ben Einstein megmutatta, hogy ha mérhető mennyiségekkel
kívánunk fizikát űzni, akkor egy esemény x, y, z helyét és t idejét a
különböző, sebességekkel mozgó megfigyelők másnak és másnak mérik, bizonyos
szabályok szerint. Eredményéről azután volt főiskolai tanára, Minkowski,
1908-ban megmutatta, hogy mit jelent. Nincs külön tér és idő. Egyetlen
4-dimenziós téridő van, melynek pontjai az események, adott helyen és
időben.
Két nagyon közeli esemény négyestávolságát (1)-hez hasonló képlet adja:
dsý = dxý + dyý + dzý - cýdtý. (5)
Ezt mindenki egyformának látja; hogy azután két esemény közt ki mennyi
teret és mennyi időt lát, az attól függ, milyen "szögből" néz rá, azaz
hogyan mozog. A részleteket legjobb Einsteintől elolvasni." De mit jelent a
fenti ds, és hogyan magyarázza meg a Michelson-kísérlet negatív eredményét?
Vegyünk először két eseményt, melyre dsý < 0. Ekkor a második esemény az
elsőből fénysebesség alatti egyenletes mozgással elérhető. Hajítsunk át
valami műszert ilyen sebességgel: legyen rajta távolságmérő és óra. A műszer
nem tudja, hogy ő mozog, tehát azt hiszi, hogy áll: x, y és z nem változik,
csak t. Ennek változását mutatja az óra. E speciálisan mozgó óra mutatta
időt sajátidőnek hívjuk, ez t, tehát
dtau = sqrt (- dsý)/c. (6)
Ha a két esemény közt dsý > 0, akkor a képlet mutatja, hogy ilyen dz
nincs. Akkor megpróbálunk úgy mozogni, hogy a kezdő- és végesemény idejét
lássuk azonosnak; akkor egy t távolságot mérhetünk köztük eme térben, és
láthatóan ds = dtau.
Nos, nézzük a 2. ábrát! Van az A és B esemény, és két űrhajós, akik
szemlélik. Az első pályája egyszerűen a függőleges tengely (hiszen áll az x
= 0 pontban); a másodiké épp átmegy a két eseményen. A dolgokat úgy írjuk
le, ahogyan az első látja. Számára a második sebessége
v = dx/dt. (7)
2. ábra.
Relativisztikus időlassulás
Két esemény (A és B) időbeli távolságát az
1. megfigyelő dt-nek méri Az egyik
eseményből a másikhoz utazó 2. űrhajós
saját óráján múló idő ehhez képest
sqrt(1-vý/cý) arányban rövidül, ahol v a 2.
sebessége az 1. mérése szerint. A
rövidülést az ábra nem tudja láttatni, mert
pszeudo-euklideszi geometriát nem lehet
euklideszi síkon mérettartóan ábrázolni.
O a két esemény közt dt időt mért, de leolvashatja a második órájáról,
hogy az mennyit mért. Az (5) és (6) képletekből:
dtau = sqrt (- dsý)/c = dt sqrt (1-vý/cý). (8)
Ezt hívják relativisztikus időlassulásnak. A gyorsan mozgó űrhajón
lassabban telik az idő, mint az induló- és célállomáson. Van egy teljesen
hasonló képlet a távolságokra is, formailag olyan, mint a Lorentz-
kontrakció, de azzal nincs dolgunk.
No, és hogyan értjük ebből meg a Michelson-kísérletet?
Egyszerűen. A fény terjedése közben dxý = cýdtý, tehát ds = 0. Ez azonban
a minden megfigyelő számára azonos négyestávolság, tehát ha egy megfigyelő
dx = cdt -t látott, a többi is azt lát. Bármelyik, bárhogy mozogva elosztja
saját mért dx-ét és dt-jét, ugyanannyit kap. A téridő léte miatt a fény
terjedési sebessége mindenkinek ugyanaz, akárhogy mozgunk, és minden
Michelson-kísérlet negatív eredményt kell adjon.
De a téridő egy elmélet. A Michelson-kísérlet egymagában nem
bizonyíthatja, hogy nincs külön tér és idő; számos más magyarázatot is ki
lehet agyalni. Közvetlenebb bizonyítékok kellenek, és azokat kicsiben
szerezzük meg.
Vegyünk egy bomlékony részecskét: valamennyi tau idő alatt bomlik, és
azalatt vtau utat tesz meg. De ha van "időlassulás", akkor eme út
vt/sqrt(1-vý/cý), mert a "kint" mért idő hosszabb tau-nál. Nos, ezt kozmikus
sugárzásban vagy gyorsítóval ellenőrizni lehet; úgy is van, [10] és a képlet
is jól.
Egy másik ellenőrzés az, hogy megpróbáljuk a részecskénket fénysebesség
fölé gyorsítani. A gyorsítóval adunk valamekkora E mozgási energiát; ez a
newtoni fizika szerint ad valamekkora sebességet, mégpedig
E = 1/2 mvý (9)
szerint, ahol m a részecske (gyorsítás előtti és utáni) tömege. Eszerint egy
elektron negyedmillió elektronvolt gyorsítóenergián elérné a fénysebességet.
A mai gyorsítók ennek a milliószorosánál (!) járnak, de fénysebesség alatt.
A speciális relativitáselmélet jelzi is, hogy nem jutunk c fölé. Végtére
is a fénysebesség átlépésekor (8) megbolondulna, és a felgyorsított óra nem
mérhetne semmit. Konkrétan az történik, hogy a mozgási energia
relativisztikus képlete (9) helyett más:
(10)
Ez végtelenhez tart, amint v a c-hez közeledik. És megint a kísérletek
összevágnak a képlettel. Ezt szokás úgy mondani, hogy a felgyorsított test
tömege m/sqrt(1-vý/cý) szerint nő, és a növekvő tömeget egyre nehezebb
gyorsítani. Mondhatjuk így is; a lényeg a (10) képlet.
Van még sok ilyen kísérlet. Legtöbb elemi részecskékre, hiszen azokat
könnyű fénysebesség tájára gyorsítani: igazolják a speciális
relativitáselméletet. Van néhány kísérlet emberi méretű tárgyakkal is: pl.
repülőgépen körbevitt atomóra tényleg lassabban járt, mint a békén hagyott.
Végül vannak egészen nagyban csillagászati megfigyelések is. Ezek legtöbbje
egyezik a relativitáselmélet jóslatával, de az általános
relativitáselméletével, mert gravitáció is jelen van. De van egy érdekes
ellenkező adat, amiről már itt szólhatunk.
A kvazárok legfeljebb Naprendszer méretű, de ahhoz képest nagy tömegű
távoli égitestek (2 milliárd fényévnél közelebb nincs belőlük).
Teljesítményük hatalmas: valószínűleg valamiféle gravitációs összeomlás
folyik bennük. [12] Sok környékén kidobott fénylő anyag látszik, és nagyon
bonyolult mérésekkel láthatóan távolodik. Ez nem volna meglepő; csakhogy van
olyan, amely 1 év alatt 1 fényévnél többel látszik elmozdulni. Ezek jól
dokumentált megfigyelések; [12] tessék, itt a fénynél gyorsabb mozgás. Nem
igaz a relativitáselmélet?
Na, ez így túlzás. Van másik magyarázat is. Ez egyszerű, de hosszadalmas.
Talán a 3. ábra segít. Az A kvazár t = 0-kor v sebességgel, a B
megfigyelőhöz a szög alatt kidobja a C anyagot. Eme esemény fénye t = R/c-
ben jut a megfigyelőhöz.
3. ábra
Szuperluminális események hagyományos magyarázata
Az A kvazár t pillanatban a B megfigyelőhöz képest ŕ szögben v
sebességgel kidob egy fénylő C anyagot, és idővel később újra
felfénylik C. Mivel C közeledik, a két eseményt mi -nál kisebb
időkülönbséggel látjuk, ezért C mozgását a valódinál gyorsabbnak
látjuk. Ha v közel van c-hez, és az a szög közepes, a látszólagos
sebesség c feletti lehet.
Valamennyi idő múlva a kidobott anyag v cos ŕ-val van a megfigyelőhöz
közelebb és v sin ŕ kitérésnyire látszik. Eme esemény fénye
+ (R - v cos ŕ)/c időkor érkezik meg. A megfigyelő látta távolodás és
időkülönbség aránya a látszó sebesség:
(11)
Ez ugyan általában az a szög csökkenésével csökken (hiszen egyre kevésbé
látszik C távolodni), de ha v csak alig kisebb c-nél, sem túl kis, sem túl
nagy ŕ szögnél v1 nagyobb lesz c-nél. Aki nem hiszi, vegyen elő
függvénytáblát: v = 0,9c esetén v1 nagyobb c-nél 7º és 83º közt, tehát
majdnem mindig, ha nem hátrafelé repül. A fénysebesség 90%-a nagy sebesség,
de nagy robbanásban nem lehetetlen; ettől kezdve a dolog számunkra addig
érdektelen, amíg a kvazárokról részleteket nem tudunk meg.
Szóval amennyire ezt le tudtuk ellenőrizni, téridő van, Minkowski-
geometria van (egészen nagyban már nem az lesz, de erről később),
fénysebesség fölé nem lehet gyorsítani. Ez nem egyszerűen a "hivatalos"
állítás; akinek nem tetszik, az álljon elő, és magyarázzon meg mindent, amit
a gyorsítókban látunk úgy, hogy lehessen c fölé menni. Végül is, sokszor
megpróbáltuk.
De akkor most már a (2) képlet nem igaz, mert ott feltettük, hogy a
sebességet lehet egyenletesen növelni akár c fölé is, és nem lehet. A
számításokat újra el kell végezni, olyan gyorsulással, amit az űrhajós érez
mindig 1 g-nek. Fénysebességhez közeledve a Földön maradt szemlélők egyre
kevésbé látják gyorsulni az űrhajót. Mégis, az űrhajós tau sajátidejében a
képlet érvényes marad. A tau-Cetire neki 7 év kell. De ezalatt a Földön 14,5
év telik el. És ezt a gyorsítás növelésével sem lehet rövidíteni. 12
fényévet a Föld számára 12 évnél hamarabb nem lehet megtenni.
Han Solo Ezredéves Sólyma a Bespint (óriási gyorsulással, utasait
befagyasztva stb.) elérhette úgy, hogy közben az űrhajóban még 1 év sem telt
el. De a Galaxisban közben elmúlt 4-5 év. Nem hiányzott közben Leia hercegnő
társainak?
És akkor most mi van a Galaktikus Vasutakkal? Hatalmas gravitációval
felgyorsíthatunk járműveket, mégsem lehet úgy közlekedni, hogy vissza is
térhessünk kortársaink életében? Hiszen ugyan minek elutazni 1000
fényévnyire és visszatérni, ha a hozott hírre már senki sem kíváncsi, magunk
meg rá sem ismerünk otthonunkra? Akkor már ott is maradhatunk, ahová
mentünk. Nos, ne siessünk. Ahol nagy gravitáció van, ott általános
relativitáselmélet kell. Majd akkor látjuk, mi van.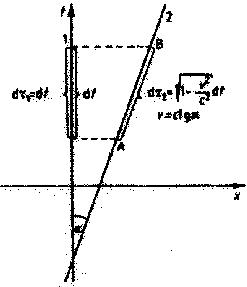
2. ábra.
Relativisztikus időlassulás
Két esemény (A és B) időbeli távolságát az
1. megfigyelő dt-nek méri Az egyik
eseményből a másikhoz utazó 2. űrhajós
saját óráján múló idő ehhez képest
sqrt(1-vý/cý) arányban rövidül, ahol v a 2.
sebessége az 1. mérése szerint. A
rövidülést az ábra nem tudja láttatni, mert
pszeudo-euklideszi geometriát nem lehet
euklideszi síkon mérettartóan ábrázolni.
O a két esemény közt dt időt mért, de leolvashatja a második órájáról,
hogy az mennyit mért. Az (5) és (6) képletekből:
dtau = sqrt (- dsý)/c = dt sqrt (1-vý/cý). (8)
Ezt hívják relativisztikus időlassulásnak. A gyorsan mozgó űrhajón
lassabban telik az idő, mint az induló- és célállomáson. Van egy teljesen
hasonló képlet a távolságokra is, formailag olyan, mint a Lorentz-
kontrakció, de azzal nincs dolgunk.
No, és hogyan értjük ebből meg a Michelson-kísérletet?
Egyszerűen. A fény terjedése közben dxý = cýdtý, tehát ds = 0. Ez azonban
a minden megfigyelő számára azonos négyestávolság, tehát ha egy megfigyelő
dx = cdt -t látott, a többi is azt lát. Bármelyik, bárhogy mozogva elosztja
saját mért dx-ét és dt-jét, ugyanannyit kap. A téridő léte miatt a fény
terjedési sebessége mindenkinek ugyanaz, akárhogy mozgunk, és minden
Michelson-kísérlet negatív eredményt kell adjon.
De a téridő egy elmélet. A Michelson-kísérlet egymagában nem
bizonyíthatja, hogy nincs külön tér és idő; számos más magyarázatot is ki
lehet agyalni. Közvetlenebb bizonyítékok kellenek, és azokat kicsiben
szerezzük meg.
Vegyünk egy bomlékony részecskét: valamennyi tau idő alatt bomlik, és
azalatt vtau utat tesz meg. De ha van "időlassulás", akkor eme út
vt/sqrt(1-vý/cý), mert a "kint" mért idő hosszabb tau-nál. Nos, ezt kozmikus
sugárzásban vagy gyorsítóval ellenőrizni lehet; úgy is van, [10] és a képlet
is jól.
Egy másik ellenőrzés az, hogy megpróbáljuk a részecskénket fénysebesség
fölé gyorsítani. A gyorsítóval adunk valamekkora E mozgási energiát; ez a
newtoni fizika szerint ad valamekkora sebességet, mégpedig
E = 1/2 mvý (9)
szerint, ahol m a részecske (gyorsítás előtti és utáni) tömege. Eszerint egy
elektron negyedmillió elektronvolt gyorsítóenergián elérné a fénysebességet.
A mai gyorsítók ennek a milliószorosánál (!) járnak, de fénysebesség alatt.
A speciális relativitáselmélet jelzi is, hogy nem jutunk c fölé. Végtére
is a fénysebesség átlépésekor (8) megbolondulna, és a felgyorsított óra nem
mérhetne semmit. Konkrétan az történik, hogy a mozgási energia
relativisztikus képlete (9) helyett más:
(10)
Ez végtelenhez tart, amint v a c-hez közeledik. És megint a kísérletek
összevágnak a képlettel. Ezt szokás úgy mondani, hogy a felgyorsított test
tömege m/sqrt(1-vý/cý) szerint nő, és a növekvő tömeget egyre nehezebb
gyorsítani. Mondhatjuk így is; a lényeg a (10) képlet.
Van még sok ilyen kísérlet. Legtöbb elemi részecskékre, hiszen azokat
könnyű fénysebesség tájára gyorsítani: igazolják a speciális
relativitáselméletet. Van néhány kísérlet emberi méretű tárgyakkal is: pl.
repülőgépen körbevitt atomóra tényleg lassabban járt, mint a békén hagyott.
Végül vannak egészen nagyban csillagászati megfigyelések is. Ezek legtöbbje
egyezik a relativitáselmélet jóslatával, de az általános
relativitáselméletével, mert gravitáció is jelen van. De van egy érdekes
ellenkező adat, amiről már itt szólhatunk.
A kvazárok legfeljebb Naprendszer méretű, de ahhoz képest nagy tömegű
távoli égitestek (2 milliárd fényévnél közelebb nincs belőlük).
Teljesítményük hatalmas: valószínűleg valamiféle gravitációs összeomlás
folyik bennük. [12] Sok környékén kidobott fénylő anyag látszik, és nagyon
bonyolult mérésekkel láthatóan távolodik. Ez nem volna meglepő; csakhogy van
olyan, amely 1 év alatt 1 fényévnél többel látszik elmozdulni. Ezek jól
dokumentált megfigyelések; [12] tessék, itt a fénynél gyorsabb mozgás. Nem
igaz a relativitáselmélet?
Na, ez így túlzás. Van másik magyarázat is. Ez egyszerű, de hosszadalmas.
Talán a 3. ábra segít. Az A kvazár t = 0-kor v sebességgel, a B
megfigyelőhöz a szög alatt kidobja a C anyagot. Eme esemény fénye t = R/c-
ben jut a megfigyelőhöz.
3. ábra
Szuperluminális események hagyományos magyarázata
Az A kvazár t pillanatban a B megfigyelőhöz képest ŕ szögben v
sebességgel kidob egy fénylő C anyagot, és idővel később újra
felfénylik C. Mivel C közeledik, a két eseményt mi -nál kisebb
időkülönbséggel látjuk, ezért C mozgását a valódinál gyorsabbnak
látjuk. Ha v közel van c-hez, és az a szög közepes, a látszólagos
sebesség c feletti lehet.
Valamennyi idő múlva a kidobott anyag v cos ŕ-val van a megfigyelőhöz
közelebb és v sin ŕ kitérésnyire látszik. Eme esemény fénye
+ (R - v cos ŕ)/c időkor érkezik meg. A megfigyelő látta távolodás és
időkülönbség aránya a látszó sebesség:
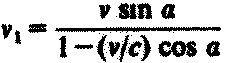(11)
Ez ugyan általában az a szög csökkenésével csökken (hiszen egyre kevésbé
látszik C távolodni), de ha v csak alig kisebb c-nél, sem túl kis, sem túl
nagy ŕ szögnél v1 nagyobb lesz c-nél. Aki nem hiszi, vegyen elő
függvénytáblát: v = 0,9c esetén v1 nagyobb c-nél 7º és 83º közt, tehát
majdnem mindig, ha nem hátrafelé repül. A fénysebesség 90%-a nagy sebesség,
de nagy robbanásban nem lehetetlen; ettől kezdve a dolog számunkra addig
érdektelen, amíg a kvazárokról részleteket nem tudunk meg.
Szóval amennyire ezt le tudtuk ellenőrizni, téridő van, Minkowski-
geometria van (egészen nagyban már nem az lesz, de erről később),
fénysebesség fölé nem lehet gyorsítani. Ez nem egyszerűen a "hivatalos"
állítás; akinek nem tetszik, az álljon elő, és magyarázzon meg mindent, amit
a gyorsítókban látunk úgy, hogy lehessen c fölé menni. Végül is, sokszor
megpróbáltuk.
De akkor most már a (2) képlet nem igaz, mert ott feltettük, hogy a
sebességet lehet egyenletesen növelni akár c fölé is, és nem lehet. A
számításokat újra el kell végezni, olyan gyorsulással, amit az űrhajós érez
mindig 1 g-nek. Fénysebességhez közeledve a Földön maradt szemlélők egyre
kevésbé látják gyorsulni az űrhajót. Mégis, az űrhajós tau sajátidejében a
képlet érvényes marad. A tau-Cetire neki 7 év kell. De ezalatt a Földön 14,5
év telik el. És ezt a gyorsítás növelésével sem lehet rövidíteni. 12
fényévet a Föld számára 12 évnél hamarabb nem lehet megtenni.
Han Solo Ezredéves Sólyma a Bespint (óriási gyorsulással, utasait
befagyasztva stb.) elérhette úgy, hogy közben az űrhajóban még 1 év sem telt
el. De a Galaxisban közben elmúlt 4-5 év. Nem hiányzott közben Leia hercegnő
társainak?
És akkor most mi van a Galaktikus Vasutakkal? Hatalmas gravitációval
felgyorsíthatunk járműveket, mégsem lehet úgy közlekedni, hogy vissza is
térhessünk kortársaink életében? Hiszen ugyan minek elutazni 1000
fényévnyire és visszatérni, ha a hozott hírre már senki sem kíváncsi, magunk
meg rá sem ismerünk otthonunkra? Akkor már ott is maradhatunk, ahová
mentünk. Nos, ne siessünk. Ahol nagy gravitáció van, ott általános
relativitáselmélet kell. Majd akkor látjuk, mi van.