TACHYONOK?
A szó gyors részecskét jelent, azaz fénynél gyorsabbat. Ugyanis a
speciális relativitáselmélet nem azt tiltja, hogy valami fénynél gyorsabb
legyen, hanem azt, hogy azzá váljon. Lehetnek olyan részecskék, melyek
mindig fénynél gyorsabbak; ha energiát kapnak, lassulnak, fénysebesség felé.
A helyzetet a 4. ábra szemlélteti. Az A esemény egy adóállomás működése: az
adó valahogyan szabályozni tudja részecskék áramlását, és ezzel ad
jelzéseket. A szaggatott vonal az A esemény fénykúpja: a kifutó fényjelek
útja, és a múltban olyan befutó fényjelek, melyek épp A-ba érnek. Normális
részecskék (amilyeneket ismerünk) a fénykúp belsejében futhatnak, és nem
tudják megelőzni a fényjeleket. A tachyonok csak a fénykúpon kívül
futhatnak. Mivel, ha más-más megfigyelők néznek egy normális részecskét,
annak sebességét -c és +c közt akárminek láthatják, azaz a fénykúp
belsejének minden egyenese egyenértékű (csak a relatív sebességnek van
értelme, az abszolútnak nincs, épp ez a relativitáselmélet). Nyilván a
tachyonok meg akárhol futhatnak a fénykúpon kívül.
4. ábra.
Normális részecskék és tachyonok
Egy "adóállomás" az A eseménynél
részecskéket bocsát ki. Az x és
t tengely az adóállomás saját
koordináta-rendszere, de ennek a
relativitáselmélet szerint nincs
jelentősége. A pontozott vonal
az A esemény fénykúpja. A kúp
felett mozognak a fénynél las-
sabb részecskék (mint amilyene-
ket ismerünk), alulról jöhetnek
be A-ba. A kúpon kívülre csak
fénysebességnél gyorsabban le-
hetne eljutni. 1. és 2. fénynél
lassabb részecske; 2. egyre
gyorsul, és megközelíti a fény-
sebességet, ahogyan energiája nő. 3., 4. és 5. tachyon: 4.
energia felvételével egyre lassul fénysebesség felé. 5. időben
visszafelé halad, ami a fénykúpon kívül nem kizárt.
Remek. Akkor végtelen sebességük is lehet, egy pillanat alatt akármilyen
messze tudunk üzenni. De tudunk-e utazni? Erre a tudományos-fantasztikus
irodalomban kétféle javaslat van. Az első: testünk mintázatát lemásoljuk
tachyonokkal, és a mintázatból újra előállunk a célnál. [13] Ötletes, de
veszélyes, és zavaró filozófiai problémákat tartalmaz: ami ugyanolyan, mint
én, az én vagyok-e, folytatja-e az az én tudatomat? Ne töprengjünk ezen: van
kispolgáribb megoldás is. Tachyonsugarakkal vezérelve gyárthatunk robotokat
a célállomáson, és azután mesterséges érzékszerveik és agyunk közt
tachyonokkal tarthatjuk a kapcsolatot. [14] Ez épp olyan, mintha ott
volnánk.
Ez remek. Csakhogy tachyonokkal üzenni lehet a múltba, az 5. ábra
szerint. A tachyonok ugyanis akárhol futhatnak a fénykúpon kívül. (A
fizikusok által vagy 20 éve ténylegesen kitalált berendezés kicsit
bonyolultabb: 4 adó-vevő kell hozzá, melyek egymáshoz képest fényhez közeli
sebességekkel mozognak, de a tisztelt olvasó e bonyodalom nélkül is el lesz
valahogyan.) Na de mi van, ha az A adóban van egy bomba, amely a
visszaérkező jelre robban? Ha A adott jelet, az a múltban visszaér,
felrobbantja a bombát, de akkor nincs jel. De ha nincs jel, nem robban a
bomba, tehát lesz jel a múltban, de akkor felrobban a bomba, tehát nincs
jel. Ebből elég. Nagy kavarodás támad, ha hírt lehet küldeni a múltba.
Ilyenen évezredek óta töprengenek. Ez ugyanis az "igazi prófécia"
kérdése. Ha a jóslás nem találgatás, hanem a jövőből jövő igazi hír, akkor
megakadályozhatja saját bekövetkeztét. A görögök nem hitték, hogy minden
jóslás igazi, de azért úgy hitték, hogy vannak igazi jósdák, pl. Delphoi.
Lássuk most szegény Oidipusz király történetét. Dehogy is volt neki
oidipusz-komplexusa; az egész történet épp az, hogyan próbálta elkerülni
saját anyját. [15]
5. ábra.
Időbeli paradoxon
tachyonokkal
Az A "tachyonadó" időben
visszafelé futó tachyont
tud kibocsátani, az üze-
netet B közvetítőállo-
másként visszasugározza,
és az még elindítása
előtt visszaér ( 1-2-3).
Ha az üzenet megakadá-
lyozza az adó működését,
akkor nem indulhatott
el. Ténylegesen javasol-
tak ilyen berendezést 4
adóvevővel, ami ilyen
képtelen módon "működ-
ne", amennyiben vannak tachyonok.
Laiosz thébai király jóslatot kap, hogy most születendő fia majd őt
megöli, és saját anyjával hál. Ezt jobb elkerülni; látszólag semmi akadálya,
a gyermeket el kell emészteni, és kész. Csakhogy senki sem mészárolja le
élvezettel saját elsőszülött fiát, meg az anyának sem tetszene a dolog. Mit
csinál? Odaadja egy szolgájának, eméssze el az. Ő is továbbadta, a második
szolga sem akart csecsemőt ölni, hát kitette a vadonba, emésszék el a vadak.
Ott viszont megtalálta a gyermektelen korinthoszi király vadásza. A csecsemő
megtetszett a királyi párnak; elhatározták, hogy titokban örökbe fogadják.
Senki nem tudhatta meg, hogy nem az övék, mert akkor jogait követelte volna
a királyság valamely távolabbi várományosa.
A kis Oidipusz felserdült; vélt szüleit nagyon szerette. Trónörökösnek
nem árt, ha jóslatot kér Delphoiban, de mikor belépett a szentélybe, a
Pythia ráförmedt: "Takarodj nyomorult. Megölöd apádat és anyáddal hálsz!".
Ezt persze jobb elkerülni, ezért már haza sem ment. (Mit is mondhatna vélt
szüleinek?) Idegenben vándorolva egy útkeresztezésnél összetűzött Laiosz
thébai királlyal, és agyonütötte. Nem tudta, hogy a thébai királlyal áll
szemben, de ha tudta volna, sem izgatja. Azután megölte a Thébát sanyargató
Szfinxet, így mire Thébába ért, hősként ünnepelték, és megtették eltűnt
királyuk, utódjának. Egyszerűség kedvéért hozzáadták az özvegy királynét is,
aki hozzá kicsit idős volt már, de még csinos. Oidipusz jöttment volt, nem
válogathatott, a királynénak semmi kifogása sem volt, az udvart meg nem
kellett megbolygatni. A megjósolt vérfertőzés így menetrend szerint
megtörtént. Gondoljuk meg: a herceget csecsemőként pillanatokig látta néhány
szolga. Nevét is Korinthoszban kapta. Az egyetlen, aki még gyanakodhatott,
hogy nem egészen biztos a csecsemő halála, valahol vidéken élt. Ki gondolta
volna róla, hogy Iokaszté királyné fia? Persze a bűn megtörtént: ezek után a
legkevesebb, hogy Apollón dögvésszel sújtsa a várost, ami meg is lett.
Nos, így vált valóra a jóslat. A konstrukció azért egy fizikusnak nem
eléggé kényszerítő erejű, legfeljebb irányt mutathat. De arra jó.
A mai fizikának súlyos nehézségei volnának időutazások vagy hátraküldött
üzenetek esetén. Az okot a 6. ábra mutatja. A fizikai hatások - legjobb
tudomásunk szerint időben előre terjednek a térben. Tegyük fel, hogy a
jövőbeli hatás valahogyan visszakerül a múltba. Onnan azután megint előre
terjed. De akkor az A eseménynél pl. az elektromágneses térerőnek két
különböző értéke lesz: az ami az "első menetben" fejlődött ki és az, ami a
másodikban. E probléma csak akkor nem lép fel, ha a térerő lent az a jelű
vonalon épp annyi, mint fent a b jelű vonalon. De honnan tudja ezt előre a
térerő? Ha az a jelű alatt volt valamilyen térerő, az a-ig valamivé
fejlődik, de általában nem pont olyanná, mint b-ben.
Nos, ezt odatehetjük az előző paradoxon mellé a magát felrobbantó
rádióadóval. Az időutazás csak zűrzavart csinál. Vannak, akik ezt annyira
komolyan veszik, hogy bizonyos fizikai elveket fogalmaznak meg (pl. a később
még említendő Kozmikus Cenzúrát), amelyek megakadályozzák az időutazást. Ez
esetben persze tachyonok sem létezhetnek (amik nem is hiányoznak senkinek).
De az én saját véleményem az, hogy egyszerűen nem tudunk még eleget az
ügyben ahhoz, hogy végleges kijelentéseket tegyünk. A paradoxon léte
kétségtelen. De lássunk egy ógörög paradoxont Zénóntól, aki azzal azt akarta
bizonyítani, hogy a mozgás fogalmával súlyos bajok vannak.
6. ábra
A jövő és múlt összekapcsoló-
dásából eredő zavar
Képünk a téridő egy olyan ré-
sze. ahol valahogyan a jövőbe-
li b vonalról a hatások visz-
szakerülnek a múltba a-ra. A
hullám terjedő elektromágne-
sesség: F az eredeti forrás és
az A eseménynél szemlélődünk.
Mivel A-t a jelek többször is
elérik, ott a térerő többérté-
kű akar lenni, ami értelmet-
len. A zavar akkor nem lép
fel, ha a és b közt a térerő
nem változik, vagy legalábbis
csak úgy teszi. hogy a-n és
b-n minden ugyanolyan legyen. A b --> a
kapcsolat befagyasztja a változásokat.
Képzeljük el, hogy Akhillész és egy teknősbéka versenyt fut.
Kétségtelenül Akhillész győz, a gyorslábú, hiszen félisteni hős (apja
Péleusz mürmidón király, anyja Thétisz istennő). De próbáljuk kiszámítani -
mondja Zénón - a verseny eredményét, pl. olyan számszerű adatokkal, hogy
Akhillész sebessége 10 m/s, a teknősé 1 m/s, és a teknős kap 10 m előnyt!
Mire Akhillész odaér, ahonnan a teknős indult, az előbbrejutott 1 m-rel.
Mire ezt is megteszi Akhillész, az előny még mindig 10 cm. És így tovább.
Nos - mondja Zénón végtelen sok lépés után is a teknős van elől, tehát
Akhillész nem előzheti meg. Viszont máshonnan tudjuk, hogy megelőzi. Itt a
paradoxon.
De figyeljünk arra, hogy Zénón nem azt állította, hogy az ilyen verseny
tilos. Nem arra következtetett, hogy ha rajthoz állnának, Zeusz atya
villámmal sújtaná le őket, hogy megőrizze a világrendet. Ő csak azt mondta,
hogy a mozgással baj van. Még ez sem volt igaz. Lássuk csak, mennyit tesz
meg Akhillész Zénón végtelen sok lépésében: 10 + 1 + 0,1 + 0,01 + ...
métert, azaz 11,1111 ... métert, más szóval 100/9 métert. Ez véges távolság,
és itt éri utol a teknőst. Utána már ő van elől, és a tapasztalat szerint ez
is történik. Csak meg kellett tanulni végtelen sorokat összegezni.
Nehogy félreértessem. Nem állítom azt, hogy fel tudom oldani az
időutazási paradoxonokat. Vannak bizonyos ötleteim, de még egyet sem
ellenőriztem le a fizikában szokásos alapossággal, hogy megoldja-e a
problémát. Félő, hogy egyik sem segít majd. Csak azt mondom, hogy
paradoxonok léte mindig azt mutatja, hogy valamit nem tudunk, vagy nem
értünk, de hogy mi az, azt nem mutatják meg. Nincs elég adatunk ahhoz, hogy
a múltba utazást kizárjuk. Lehet, hogy majd ki kell zárni, de most
feltesszük, hogy tiltó elv nincs.
Akkor is, a múltra visszahatás nem lehet tömeges és általános. Akkor
ugyanis, mint láttuk a 6. ábrán, az alsó és felső kapcsolat közt a
változások (csaknem teljesen) megszűnnének, a világ ott befagyna. A világ
pedig nem fagyott be, legalábbis itt nálunk nem.
Nos, lássuk a tachyonokat! Fizikáról volna szó, hát most ne töprengjünk;
keressük őket! Miről lehetne felismerni őket: arról, hogy fénynél
gyorsabbak. Tegyük fel, hogy van elektromos töltésük (valamilyen töltésük
csak illene legyen); a fénynél gyorsabb töltések jellegzetes ún. Cserenkov-
fénysugárzást bocsátanak ki. (Hogy honnan tudjuk? Egyrészt az
elektrodinamika egyenleteit c-nél gyorsabban mozgó töltésre is meg tudjuk
oldani, másrészt vízben megelőzheti egy elektron a fényt, és ott látjuk is a
sugárzást.) Keressük ezt!
Megpróbálták, eredménytelenül. [16] Próbáltak még néhány módon
tachyonokat látni, de nem láttak. Három lehetőség van:
l. tachyonok nincsenek;
2. vannak, de nem hathatnak kölcsön a normális anyaggal;
3. kölcsön is hatnak, de gyengén, és ritkák.
Az első két eset közt számunkra semmi különbség nincs. A harmadik
fenntart bizonyos esélyeket, de most már egyszer lehetünk szigorúak is. A
tachyonok létét az elmélet nem jósolta, csak épp, esetleg, megengedte.
Bajokat okozhatnak. Megpróbáltuk észlelni őket, de nem mutatkoztak. A
továbbiakban, a kísérlet negatív eredményére támaszkodva, felteszem, hogy
nincsenek. Akinek ez nem tetszik, mutasson bármiféle rájuk utaló jelet,
akkor visszatérhetünk rájuk.
Node akkor nincs is időutazás ugye? Ahhoz, hogy egy részecskét
visszafordíthassunk az időben, ahhoz pályáját előbb ki kell hajlítani a
fénykúpból (4. ábra), az meg nem megy az elmélet és a gyorsítós kísérletek
szerint. Csakhogy: úgy is lehet hátra jutni, hogy mindig előre megyünk.
Kolumbusz is Nyugat felé ment Keletre, és csak azért nem érte el, mert
közben volt Amerika.
Ehhez a téridőnek nem egyszeresen összefüggőnek kell lennie. Ez egy
gyönyörű matematikai szakkifejezés, de jobb, ha aprópénzre váltjuk, a 7.
ábra szerint. Vegyünk egy sík felületet, pl. egy milliméterpapírt, és
hajtsuk önmaga alá S alakban. A benne élő síklények ezt észre sem veszik,
mert rá merőlegesen nem tudnak mozogni, a felület geometriája meg
változatlan. (A kockázás nem torzult.) Most vágjunk két lyukat A-nál és B-
nél, és oda ragasszunk be egy kis nyelvet vagy csövet! Lett egy
hátsólépcsőnk. Az A-nál lévő lyuk környékéről B környékére két úton lehet
most eljutni: a hosszabb "rendes" úton, és a rövidebb "lépcsőn". És ezt meg
tudjuk úgy csinálni, hogy a helyi geometria mindenhol sík maradjon.
7. ábra.
Hátsólépcső a sik papíron
A papírt torzulás nélkül maga alá hajthatjuk (felül: oldalnézet;
alul: felülnézet, a folytonos vonalakat látjuk, a szaggatott a
második réteg, a pontozott a harmadik). A-nál és B-nél lyukat
vágva és oda egy nyelvet ragasztva A környékéről B környékére
vezet egy rövid út. Mivel a papír négyzethálója a hajtogatástól
nem torzul, térképet kiterítve is rajzolhatunk, és ez majdnak
mindentt mérethelyes, de az A és B közti alagút a látszólagosnál
sokkal rövidebb. Helyleg mérve a geometria mindenütt a síklapé.
Namost csináljuk meg ugyanezt a téridőn, azután - mivel a görbületlen
világban észre sem vesszük a hajlatot - térképkészítés végett "simítsuk ki".
Ez a 8. ábra; csak azt kell lenyelni, hogy az A és B közt szaggatottan
rajzolt "hátsólépcső" sokkal rövidebb, mint látszik. Két ábránk azért van,
mert a két lyuk lehet térben vagy időben elválasztott, és ez két különböző
eset lesz. (Hogy azután a lyukak "kerekek"-e, vagy "hosszúkásak" és
merrefelé, az gyakorlati különbség, nem elvi.) Ezek csak a legegyszerűbb
rendellenességek; lehetnek pl. vetődések, mikor a papírt valahol felvágjuk,
egy részét eldobjuk, és elcsúsztatva ragasztjuk össze (az ilyent a
szilárdtest-fizikusok diszlokációnak hívják; ott persze időről szó sincs).
De most ez is elég lesz.
Nos, a 8. ábra a) része szerinti téridő tartományban vissza lehet jutni a
múltba, és ugyanakkor lehet gyorsan is közlekedni. Gravitációs gyorsítással
hatalmasan felgyorsítunk, csaknem fénysebességgel elrepülünk a későbbi
lyukig. Ezalatt az űrhajóban alig múlik az idő, de az induló és célállomáson
igen. Csakhogy alul kijőve vissza lehet nyerni az elmúlt időt. A 8. ábra b)
része szerint csak űrutazni lehet, de azt még egyszerűbben. Balról
odamegyünk az A lyukhoz, bemegyünk, és hipp-hopp már kint is vagyunk 100
fényévvel odébb B-nél. Ismétlem: ilyen lyukakat és alagutakat úgy is lehet
csinálni, hogy az (5) Minkowski-geometria helyileg mindenhol változatlan
maradjon; ekkor laboratóriumban semmit sem látni (hacsak épp ott nincs egy
lyuk), csillagászati megfigyelésekben pedig csak akkor látnók, ha a fény
véletlenül belemenne, ami ritka, ha kicsi a lyuk.
8. ábra.
Lehetséges (?) alagutak sík téridőn
Az a) esetben az alagút időirányba húzódik. Mivel "hátul" a sík
visszatér, időben előre haladva vissza lehet jutni. A pontozott
vonalon belül juthat valaki saját múltjába, tehát ott várhatóak
furcsaságok. A folytonos vonal egy űrhajós, aki az alagúton át
látszólag fénysebességnél gyorsabban utazik. A b) esetben az
alagút térben fut, időbeli zavarokat nem okoz, de az űrutazást
segíti. A téridő helyileg mindenütt sík. Az a) esetnek megfelelő
geometria kifejlődésének lehetőségét a specialisták vitatják.
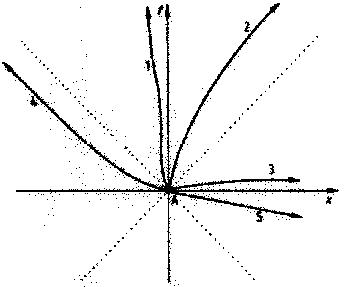4. ábra.
Normális részecskék és tachyonok
Egy "adóállomás" az A eseménynél
részecskéket bocsát ki. Az x és
t tengely az adóállomás saját
koordináta-rendszere, de ennek a
relativitáselmélet szerint nincs
jelentősége. A pontozott vonal
az A esemény fénykúpja. A kúp
felett mozognak a fénynél las-
sabb részecskék (mint amilyene-
ket ismerünk), alulról jöhetnek
be A-ba. A kúpon kívülre csak
fénysebességnél gyorsabban le-
hetne eljutni. 1. és 2. fénynél
lassabb részecske; 2. egyre
gyorsul, és megközelíti a fény-
sebességet, ahogyan energiája nő. 3., 4. és 5. tachyon: 4.
energia felvételével egyre lassul fénysebesség felé. 5. időben
visszafelé halad, ami a fénykúpon kívül nem kizárt.
Remek. Akkor végtelen sebességük is lehet, egy pillanat alatt akármilyen
messze tudunk üzenni. De tudunk-e utazni? Erre a tudományos-fantasztikus
irodalomban kétféle javaslat van. Az első: testünk mintázatát lemásoljuk
tachyonokkal, és a mintázatból újra előállunk a célnál. [13] Ötletes, de
veszélyes, és zavaró filozófiai problémákat tartalmaz: ami ugyanolyan, mint
én, az én vagyok-e, folytatja-e az az én tudatomat? Ne töprengjünk ezen: van
kispolgáribb megoldás is. Tachyonsugarakkal vezérelve gyárthatunk robotokat
a célállomáson, és azután mesterséges érzékszerveik és agyunk közt
tachyonokkal tarthatjuk a kapcsolatot. [14] Ez épp olyan, mintha ott
volnánk.
Ez remek. Csakhogy tachyonokkal üzenni lehet a múltba, az 5. ábra
szerint. A tachyonok ugyanis akárhol futhatnak a fénykúpon kívül. (A
fizikusok által vagy 20 éve ténylegesen kitalált berendezés kicsit
bonyolultabb: 4 adó-vevő kell hozzá, melyek egymáshoz képest fényhez közeli
sebességekkel mozognak, de a tisztelt olvasó e bonyodalom nélkül is el lesz
valahogyan.) Na de mi van, ha az A adóban van egy bomba, amely a
visszaérkező jelre robban? Ha A adott jelet, az a múltban visszaér,
felrobbantja a bombát, de akkor nincs jel. De ha nincs jel, nem robban a
bomba, tehát lesz jel a múltban, de akkor felrobban a bomba, tehát nincs
jel. Ebből elég. Nagy kavarodás támad, ha hírt lehet küldeni a múltba.
Ilyenen évezredek óta töprengenek. Ez ugyanis az "igazi prófécia"
kérdése. Ha a jóslás nem találgatás, hanem a jövőből jövő igazi hír, akkor
megakadályozhatja saját bekövetkeztét. A görögök nem hitték, hogy minden
jóslás igazi, de azért úgy hitték, hogy vannak igazi jósdák, pl. Delphoi.
Lássuk most szegény Oidipusz király történetét. Dehogy is volt neki
oidipusz-komplexusa; az egész történet épp az, hogyan próbálta elkerülni
saját anyját. [15]
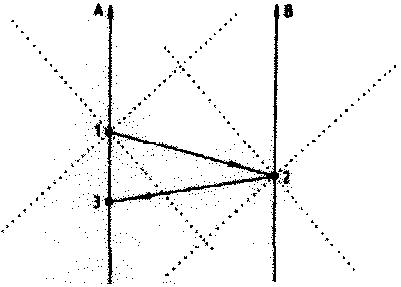5. ábra.
Időbeli paradoxon
tachyonokkal
Az A "tachyonadó" időben
visszafelé futó tachyont
tud kibocsátani, az üze-
netet B közvetítőállo-
másként visszasugározza,
és az még elindítása
előtt visszaér ( 1-2-3).
Ha az üzenet megakadá-
lyozza az adó működését,
akkor nem indulhatott
el. Ténylegesen javasol-
tak ilyen berendezést 4
adóvevővel, ami ilyen
képtelen módon "működ-
ne", amennyiben vannak tachyonok.
Laiosz thébai király jóslatot kap, hogy most születendő fia majd őt
megöli, és saját anyjával hál. Ezt jobb elkerülni; látszólag semmi akadálya,
a gyermeket el kell emészteni, és kész. Csakhogy senki sem mészárolja le
élvezettel saját elsőszülött fiát, meg az anyának sem tetszene a dolog. Mit
csinál? Odaadja egy szolgájának, eméssze el az. Ő is továbbadta, a második
szolga sem akart csecsemőt ölni, hát kitette a vadonba, emésszék el a vadak.
Ott viszont megtalálta a gyermektelen korinthoszi király vadásza. A csecsemő
megtetszett a királyi párnak; elhatározták, hogy titokban örökbe fogadják.
Senki nem tudhatta meg, hogy nem az övék, mert akkor jogait követelte volna
a királyság valamely távolabbi várományosa.
A kis Oidipusz felserdült; vélt szüleit nagyon szerette. Trónörökösnek
nem árt, ha jóslatot kér Delphoiban, de mikor belépett a szentélybe, a
Pythia ráförmedt: "Takarodj nyomorult. Megölöd apádat és anyáddal hálsz!".
Ezt persze jobb elkerülni, ezért már haza sem ment. (Mit is mondhatna vélt
szüleinek?) Idegenben vándorolva egy útkeresztezésnél összetűzött Laiosz
thébai királlyal, és agyonütötte. Nem tudta, hogy a thébai királlyal áll
szemben, de ha tudta volna, sem izgatja. Azután megölte a Thébát sanyargató
Szfinxet, így mire Thébába ért, hősként ünnepelték, és megtették eltűnt
királyuk, utódjának. Egyszerűség kedvéért hozzáadták az özvegy királynét is,
aki hozzá kicsit idős volt már, de még csinos. Oidipusz jöttment volt, nem
válogathatott, a királynénak semmi kifogása sem volt, az udvart meg nem
kellett megbolygatni. A megjósolt vérfertőzés így menetrend szerint
megtörtént. Gondoljuk meg: a herceget csecsemőként pillanatokig látta néhány
szolga. Nevét is Korinthoszban kapta. Az egyetlen, aki még gyanakodhatott,
hogy nem egészen biztos a csecsemő halála, valahol vidéken élt. Ki gondolta
volna róla, hogy Iokaszté királyné fia? Persze a bűn megtörtént: ezek után a
legkevesebb, hogy Apollón dögvésszel sújtsa a várost, ami meg is lett.
Nos, így vált valóra a jóslat. A konstrukció azért egy fizikusnak nem
eléggé kényszerítő erejű, legfeljebb irányt mutathat. De arra jó.
A mai fizikának súlyos nehézségei volnának időutazások vagy hátraküldött
üzenetek esetén. Az okot a 6. ábra mutatja. A fizikai hatások - legjobb
tudomásunk szerint időben előre terjednek a térben. Tegyük fel, hogy a
jövőbeli hatás valahogyan visszakerül a múltba. Onnan azután megint előre
terjed. De akkor az A eseménynél pl. az elektromágneses térerőnek két
különböző értéke lesz: az ami az "első menetben" fejlődött ki és az, ami a
másodikban. E probléma csak akkor nem lép fel, ha a térerő lent az a jelű
vonalon épp annyi, mint fent a b jelű vonalon. De honnan tudja ezt előre a
térerő? Ha az a jelű alatt volt valamilyen térerő, az a-ig valamivé
fejlődik, de általában nem pont olyanná, mint b-ben.
Nos, ezt odatehetjük az előző paradoxon mellé a magát felrobbantó
rádióadóval. Az időutazás csak zűrzavart csinál. Vannak, akik ezt annyira
komolyan veszik, hogy bizonyos fizikai elveket fogalmaznak meg (pl. a később
még említendő Kozmikus Cenzúrát), amelyek megakadályozzák az időutazást. Ez
esetben persze tachyonok sem létezhetnek (amik nem is hiányoznak senkinek).
De az én saját véleményem az, hogy egyszerűen nem tudunk még eleget az
ügyben ahhoz, hogy végleges kijelentéseket tegyünk. A paradoxon léte
kétségtelen. De lássunk egy ógörög paradoxont Zénóntól, aki azzal azt akarta
bizonyítani, hogy a mozgás fogalmával súlyos bajok vannak.
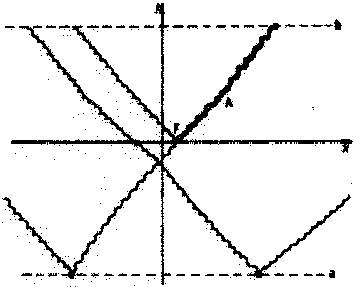6. ábra
A jövő és múlt összekapcsoló-
dásából eredő zavar
Képünk a téridő egy olyan ré-
sze. ahol valahogyan a jövőbe-
li b vonalról a hatások visz-
szakerülnek a múltba a-ra. A
hullám terjedő elektromágne-
sesség: F az eredeti forrás és
az A eseménynél szemlélődünk.
Mivel A-t a jelek többször is
elérik, ott a térerő többérté-
kű akar lenni, ami értelmet-
len. A zavar akkor nem lép
fel, ha a és b közt a térerő
nem változik, vagy legalábbis
csak úgy teszi. hogy a-n és
b-n minden ugyanolyan legyen. A b --> a
kapcsolat befagyasztja a változásokat.
Képzeljük el, hogy Akhillész és egy teknősbéka versenyt fut.
Kétségtelenül Akhillész győz, a gyorslábú, hiszen félisteni hős (apja
Péleusz mürmidón király, anyja Thétisz istennő). De próbáljuk kiszámítani -
mondja Zénón - a verseny eredményét, pl. olyan számszerű adatokkal, hogy
Akhillész sebessége 10 m/s, a teknősé 1 m/s, és a teknős kap 10 m előnyt!
Mire Akhillész odaér, ahonnan a teknős indult, az előbbrejutott 1 m-rel.
Mire ezt is megteszi Akhillész, az előny még mindig 10 cm. És így tovább.
Nos - mondja Zénón végtelen sok lépés után is a teknős van elől, tehát
Akhillész nem előzheti meg. Viszont máshonnan tudjuk, hogy megelőzi. Itt a
paradoxon.
De figyeljünk arra, hogy Zénón nem azt állította, hogy az ilyen verseny
tilos. Nem arra következtetett, hogy ha rajthoz állnának, Zeusz atya
villámmal sújtaná le őket, hogy megőrizze a világrendet. Ő csak azt mondta,
hogy a mozgással baj van. Még ez sem volt igaz. Lássuk csak, mennyit tesz
meg Akhillész Zénón végtelen sok lépésében: 10 + 1 + 0,1 + 0,01 + ...
métert, azaz 11,1111 ... métert, más szóval 100/9 métert. Ez véges távolság,
és itt éri utol a teknőst. Utána már ő van elől, és a tapasztalat szerint ez
is történik. Csak meg kellett tanulni végtelen sorokat összegezni.
Nehogy félreértessem. Nem állítom azt, hogy fel tudom oldani az
időutazási paradoxonokat. Vannak bizonyos ötleteim, de még egyet sem
ellenőriztem le a fizikában szokásos alapossággal, hogy megoldja-e a
problémát. Félő, hogy egyik sem segít majd. Csak azt mondom, hogy
paradoxonok léte mindig azt mutatja, hogy valamit nem tudunk, vagy nem
értünk, de hogy mi az, azt nem mutatják meg. Nincs elég adatunk ahhoz, hogy
a múltba utazást kizárjuk. Lehet, hogy majd ki kell zárni, de most
feltesszük, hogy tiltó elv nincs.
Akkor is, a múltra visszahatás nem lehet tömeges és általános. Akkor
ugyanis, mint láttuk a 6. ábrán, az alsó és felső kapcsolat közt a
változások (csaknem teljesen) megszűnnének, a világ ott befagyna. A világ
pedig nem fagyott be, legalábbis itt nálunk nem.
Nos, lássuk a tachyonokat! Fizikáról volna szó, hát most ne töprengjünk;
keressük őket! Miről lehetne felismerni őket: arról, hogy fénynél
gyorsabbak. Tegyük fel, hogy van elektromos töltésük (valamilyen töltésük
csak illene legyen); a fénynél gyorsabb töltések jellegzetes ún. Cserenkov-
fénysugárzást bocsátanak ki. (Hogy honnan tudjuk? Egyrészt az
elektrodinamika egyenleteit c-nél gyorsabban mozgó töltésre is meg tudjuk
oldani, másrészt vízben megelőzheti egy elektron a fényt, és ott látjuk is a
sugárzást.) Keressük ezt!
Megpróbálták, eredménytelenül. [16] Próbáltak még néhány módon
tachyonokat látni, de nem láttak. Három lehetőség van:
l. tachyonok nincsenek;
2. vannak, de nem hathatnak kölcsön a normális anyaggal;
3. kölcsön is hatnak, de gyengén, és ritkák.
Az első két eset közt számunkra semmi különbség nincs. A harmadik
fenntart bizonyos esélyeket, de most már egyszer lehetünk szigorúak is. A
tachyonok létét az elmélet nem jósolta, csak épp, esetleg, megengedte.
Bajokat okozhatnak. Megpróbáltuk észlelni őket, de nem mutatkoztak. A
továbbiakban, a kísérlet negatív eredményére támaszkodva, felteszem, hogy
nincsenek. Akinek ez nem tetszik, mutasson bármiféle rájuk utaló jelet,
akkor visszatérhetünk rájuk.
Node akkor nincs is időutazás ugye? Ahhoz, hogy egy részecskét
visszafordíthassunk az időben, ahhoz pályáját előbb ki kell hajlítani a
fénykúpból (4. ábra), az meg nem megy az elmélet és a gyorsítós kísérletek
szerint. Csakhogy: úgy is lehet hátra jutni, hogy mindig előre megyünk.
Kolumbusz is Nyugat felé ment Keletre, és csak azért nem érte el, mert
közben volt Amerika.
Ehhez a téridőnek nem egyszeresen összefüggőnek kell lennie. Ez egy
gyönyörű matematikai szakkifejezés, de jobb, ha aprópénzre váltjuk, a 7.
ábra szerint. Vegyünk egy sík felületet, pl. egy milliméterpapírt, és
hajtsuk önmaga alá S alakban. A benne élő síklények ezt észre sem veszik,
mert rá merőlegesen nem tudnak mozogni, a felület geometriája meg
változatlan. (A kockázás nem torzult.) Most vágjunk két lyukat A-nál és B-
nél, és oda ragasszunk be egy kis nyelvet vagy csövet! Lett egy
hátsólépcsőnk. Az A-nál lévő lyuk környékéről B környékére két úton lehet
most eljutni: a hosszabb "rendes" úton, és a rövidebb "lépcsőn". És ezt meg
tudjuk úgy csinálni, hogy a helyi geometria mindenhol sík maradjon.
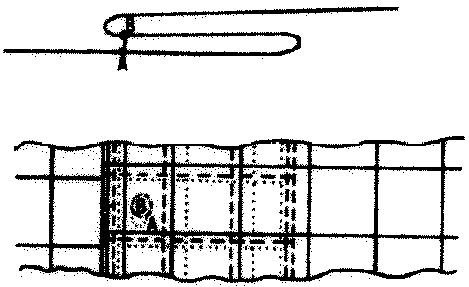7. ábra.
Hátsólépcső a sik papíron
A papírt torzulás nélkül maga alá hajthatjuk (felül: oldalnézet;
alul: felülnézet, a folytonos vonalakat látjuk, a szaggatott a
második réteg, a pontozott a harmadik). A-nál és B-nél lyukat
vágva és oda egy nyelvet ragasztva A környékéről B környékére
vezet egy rövid út. Mivel a papír négyzethálója a hajtogatástól
nem torzul, térképet kiterítve is rajzolhatunk, és ez majdnak
mindentt mérethelyes, de az A és B közti alagút a látszólagosnál
sokkal rövidebb. Helyleg mérve a geometria mindenütt a síklapé.
Namost csináljuk meg ugyanezt a téridőn, azután - mivel a görbületlen
világban észre sem vesszük a hajlatot - térképkészítés végett "simítsuk ki".
Ez a 8. ábra; csak azt kell lenyelni, hogy az A és B közt szaggatottan
rajzolt "hátsólépcső" sokkal rövidebb, mint látszik. Két ábránk azért van,
mert a két lyuk lehet térben vagy időben elválasztott, és ez két különböző
eset lesz. (Hogy azután a lyukak "kerekek"-e, vagy "hosszúkásak" és
merrefelé, az gyakorlati különbség, nem elvi.) Ezek csak a legegyszerűbb
rendellenességek; lehetnek pl. vetődések, mikor a papírt valahol felvágjuk,
egy részét eldobjuk, és elcsúsztatva ragasztjuk össze (az ilyent a
szilárdtest-fizikusok diszlokációnak hívják; ott persze időről szó sincs).
De most ez is elég lesz.
Nos, a 8. ábra a) része szerinti téridő tartományban vissza lehet jutni a
múltba, és ugyanakkor lehet gyorsan is közlekedni. Gravitációs gyorsítással
hatalmasan felgyorsítunk, csaknem fénysebességgel elrepülünk a későbbi
lyukig. Ezalatt az űrhajóban alig múlik az idő, de az induló és célállomáson
igen. Csakhogy alul kijőve vissza lehet nyerni az elmúlt időt. A 8. ábra b)
része szerint csak űrutazni lehet, de azt még egyszerűbben. Balról
odamegyünk az A lyukhoz, bemegyünk, és hipp-hopp már kint is vagyunk 100
fényévvel odébb B-nél. Ismétlem: ilyen lyukakat és alagutakat úgy is lehet
csinálni, hogy az (5) Minkowski-geometria helyileg mindenhol változatlan
maradjon; ekkor laboratóriumban semmit sem látni (hacsak épp ott nincs egy
lyuk), csillagászati megfigyelésekben pedig csak akkor látnók, ha a fény
véletlenül belemenne, ami ritka, ha kicsi a lyuk.
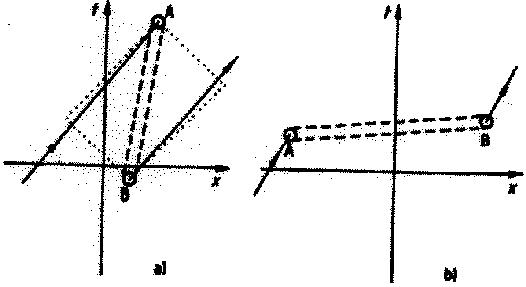8. ábra.
Lehetséges (?) alagutak sík téridőn
Az a) esetben az alagút időirányba húzódik. Mivel "hátul" a sík
visszatér, időben előre haladva vissza lehet jutni. A pontozott
vonalon belül juthat valaki saját múltjába, tehát ott várhatóak
furcsaságok. A folytonos vonal egy űrhajós, aki az alagúton át
látszólag fénysebességnél gyorsabban utazik. A b) esetben az
alagút térben fut, időbeli zavarokat nem okoz, de az űrutazást
segíti. A téridő helyileg mindenütt sík. Az a) esetnek megfelelő
geometria kifejlődésének lehetőségét a specialisták vitatják.